
如图,已知平面内有两条直线AB、CD,且 AB∥CD,P为一动点.
AB∥CD,P为一动点.
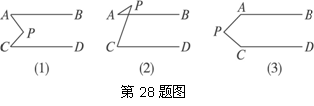 |
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.
(2)当点P移动到AB的外侧时,如图(2),是否仍有(1)的结论?如果不是__ ______________,请写出你的猜想(不要求证明).
______________,请写出你的猜想(不要求证明).
(3)当点P移动到如图(3)的位置时,∠P与∠A、∠C又有怎样的关系?能否利用(1)的结论来证明?还有其他的方法吗?请写出一种.
证明:(1)∠P=∠A+∠C,延长AP交CD与点E.
∵AB∥CD,∴∠A=∠AEC.
又∵∠APC是△PCE的外角,∴∠APC=∠C+∠AEC.∴∠APC=∠A+∠C.
(2)否;∠P=∠A-∠C.
(3)∠P=360°-(∠A+∠C).
①延长BA到E,延长DC到F,
由(1)得∠P=∠PAE+∠PCF.
∵∠PAE=180°-∠PAB,∠PCF=180°-∠PCD,
∴∠P=360°-(∠PAB+∠PCD).
②连结AC.
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵∠PAC+∠PCA=180°-∠P,
∵∠CAB+∠ACD+∠PAC+∠PCA=360°-∠P,即∠P =360°-(∠PAB+∠PCD).
=360°-(∠PAB+∠PCD).


科目:初中数学 来源: 题型:
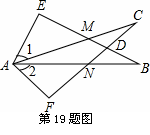
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;
③△ACN≌△ABM;④CD=DN.其中正确的结论是 (将你认为正确的结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
有一群猴子,一天结伴去偷桃子.分桃子时,如果每只猴子分3个,那么还剩下59个;如果每只猴子分5个,就都分得桃子,但有一只猴子分得的桃子不够5个.你能求出有几只猴子,几个桃子吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两人玩扑克牌游戏,游戏规则是:从牌面数字分别为5、6、7的三张扑克牌中,随机
抽取一张,放回后,再随机抽取一张,若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽取的两张牌面数字的积为偶数,则乙获胜,这个游戏___________.(填“公平”或“不公平”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com