
分析 (1)由抛物线解析式可求得开口方向、对称轴、顶点坐标及最值;
(2)把A、B、C三点的坐标分别代入解析式可求得y1、y2、y3的值,可比较其大小.
解答 解:
(1)∵y=-$\frac{1}{12}$(x-2)2+5,
∴抛物线开口向下,对称轴为x=2,顶点坐标为(2,5),当x=2时,函数有最大值,最大值为5;
(2)∵A(-6,y1),B(1,y2),C(4,y3)均在函数图象上,
∴y1=-$\frac{1}{12}$×(-6-2)2+5=-$\frac{1}{3}$,y2=-$\frac{1}{12}$×(1-2)2+5=$\frac{59}{12}$,y3=-$\frac{1}{12}$×(4-1)2+5=$\frac{51}{12}$,
∵-$\frac{1}{3}$<$\frac{51}{12}$<$\frac{59}{12}$,
∴y1<y3<y2.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从3+2x=2可得到2x=5 | |
| B. | 从6x=2x-1可得到6x-2x=-1 | |
| C. | 从$\frac{x}{2}$-1=$\frac{x-2}{3}$可得到3x-1=2(x-2) | |
| D. | 从21%+50%(60-x)=60×42%可得到21+50(60-x)=6000×42 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
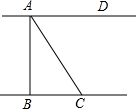 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=70°,测得BC=7m,则桥长AB=19m(结果精确到1m).
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=70°,测得BC=7m,则桥长AB=19m(结果精确到1m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 对称轴为x=3 | ||
| C. | 顶点坐标为(-3,2) | D. | 当x≥3时,y随x增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6分 | B. | 7分 | C. | 8分 | D. | 9分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
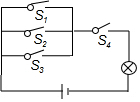 如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )
如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com