
【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题: 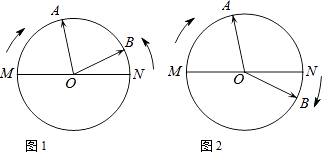
(1)若OA顺时针转动,OB逆时针转动,t=秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB=°;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?
【答案】
(1)9
(2)160
【解析】解:(1)设t秒后第一次重合.则(15+5)t=180,t=9.故答案为9.(2)①如图2中,t=2时,∠AOM=30°,∠AON=150°,∠BON=10°,∴∠AOB=∠AON+∠NOB=160°.故答案为160.②设t秒后第一次重合.由题意15t﹣5t=180,解得t=18.∴t=18秒时,第一次重合.③设t秒后∠AOB=30°,由题意15t﹣5t=150°或15t﹣5t=210°,∴t=15或21.∴t=15或18秒时,∠AOB=30°.
(1)设t秒后第一次重合.则(15+5)t=180,解方程即可.(2)①根据∠AOB=∠AON+∠NOB,求出∠AON、∠NOB即可.②设t秒后第一次重合.由题意15t﹣5t=180,解方程即可.③设t秒后∠AOB=30°,由题意15t﹣5t=150°或15t﹣5t=210°,解方程即可.


科目:初中数学 来源: 题型:
【题目】计算:
(1)-x5·x2·x10;
(2)(-2)9×(-2)8×(-2)3;
(3)a6·a2+a5·a3-2a·a7;
(4)(-a)2·(-a)3·a6.
查看答案和解析>>
科目:初中数学 来源: 题型:
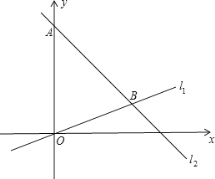
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式;
(2)点C为线段OB上一动点 (点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示);
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
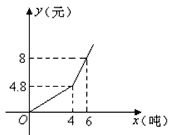
(1)分别求出当0≤x≤4、x>4时函数的解析式;
(2)当0≤x≤4、x>4时,每吨水的价格分别是多少?
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
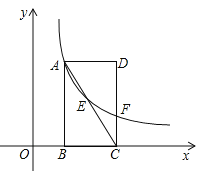
(1)点C的坐标 ;
(2)若反比例函数![]() 的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在直线AB上找一点P,使得![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com