
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
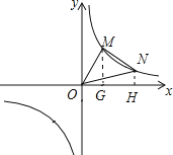
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
【答案】(1)y=-x-3;(2)m2+n2=13;(3)S△MON=3
【解析】
(1)先求得A、B的坐标,然后根据待定系数法求解即可;
(2)由点P与点Q关于x轴对称可得点Q的坐标,然后根据图象上点的坐标特征可求得mn=2,n=m+3,然后代入所求式子整理化简即得结果;
(3)如图,过M作MG⊥x轴于G,过N作NH⊥x轴于H,根据反比例函数系数k的几何意义,利用S△MON=S梯形MNHG+S△MOG-S△NOH=S梯形MNHG即可求得结果.
解:(1)∵反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1,
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1,
∴A(﹣1,﹣2),B(﹣2,﹣1),
设一次函数的表达式为y=kx+b,把A(﹣1,﹣2),B(﹣2,﹣1)代入,得:
![]() ,解得
,解得![]() ,
,
∴这个一次函数的表达式为y=﹣x﹣3;
(2)∵点P(m,n)与点Q关于x轴对称,∴Q(m,-n),
∵点P(m,n)在反比例函数图象上,∴mn=2,
∵点Q恰好落在一次函数的图象上,∴﹣n=﹣m﹣3,即n=m+3,
∴m(m+3)=2,∴m2+3m=2,
∴m2+n2=m2+(m+3)2=2m2+6m+9=2(m2+3m)+9=2×2+9=13;
(3)如图,过M作MG⊥x轴于G,过N作NH⊥x轴于H,
∵M(x1,y1),N(x2,y2)是反比例函数y=![]() 在第一象限图象上的两点,
在第一象限图象上的两点,
∴S△MOG=S△NOH=![]() =1,
=1,
∵x2-x1=2,y1+y2=3,
∴S△MON=S梯形MNHG+S△MOG-S△NOH=S梯形MNHG=![]() =
=![]() =3.
=3.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二氧化碳气体的密度 ρ(kg/m 3)与体积 V(m 3)的反比例函数关系式是![]() .
.
(1)求当 V=5m 3时二氧化碳的密度 ρ;
(2)请写出二氧化碳的密度 ρ随体积 V的增大(或减小)而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她骑车速度最快是在什么时候?车速多少?
(3)玲玲自离家到返回的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=![]() 中,x取x≠-1的实数
中,x取x≠-1的实数
C.y=![]() 中,x取x≥2的实数
中,x取x≥2的实数
D.y=![]() 中,x取x≥-3的实数
中,x取x≥-3的实数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于给定的两点![]() ,若存在点
,若存在点![]() ,使得三角形
,使得三角形![]() 的面积等于1,则称点
的面积等于1,则称点![]() 为线段
为线段![]() 的“单位面积点”. 已知在平面直角坐标系中,
的“单位面积点”. 已知在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() . 若将线段
. 若将线段![]() 沿
沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度,使得线段
个单位长度,使得线段![]() 上存在线段
上存在线段![]() 的“单位面积点”,则
的“单位面积点”,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
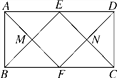
A. 正方形 B. 菱形 C. 矩形 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在等边三角形![]() 中,
中,![]() 是
是![]() 边上的动点,以
边上的动点,以![]() 为一边,向上作等边三角形
为一边,向上作等边三角形![]() ,连接
,连接![]() .
.
(1)![]() 和
和![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)试说明:![]() ;
;
(3)如图(2),将动点![]() 运动到边
运动到边![]() 的延长线上,所作三角形
的延长线上,所作三角形![]() 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com