

分析 (1)求得OB的长,则P到O的时间就可求得,进而求得OP的长;
(2)点N在AB上,PQ=2,则PN=QM=$\frac{3}{2}$PQ,据此即可求得;
(3)首先求得P在OE上,且MN在AB上时t的值,以及P在DE上,且MN在AN上时t的值,然后分情况进行讨论即可求解;
(4)过K作KG⊥NP于点G,当PK=KN'时,PG=N'G,从而求得t;当PN'=PK时,利用勾股定理求得PK,然后列方程求得t.
解答 解:(1)OB=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{2}$cm,
则点P从点B运动到点O所需的时间是$\frac{2\sqrt{2}}{\sqrt{2}}$=2,
则点P在线段OE上运动时,线段OP的长是:t-2.
故答案是2,t-2;
(2)当点N落在AB边上时,P在OE上,则PQ=$\frac{1}{2}$CD=$\frac{1}{2}$BC=2,
则PN=QM=$\frac{3}{2}$PQ=3=t,
解得:t=3.
当MN在AB上,P在CD上时,$\frac{3}{2}$(t-2)=4,
解得:t=$\frac{14}{3}$.
故答案是:$\frac{14}{3}$或3;
(3)P从B到O的时间是2秒,则BQ=t,
重合部分是△BPQ,则S=$\frac{1}{2}$t2;
当2<t≤3时,如图2.
S△OBC=$\frac{1}{4}$×42=4,QC=4-t,
则S△QCG=$\frac{1}{2}$(4-t)2,
则S=4-$\frac{1}{2}$(4-t)2=-$\frac{1}{2}$t2+4t-4;
当3<t≤4时,如图3, QM=3,BQ=t,
QM=3,BQ=t,
则QC=4-t,则S△QCG=$\frac{1}{2}$(4-t)2,
BM=t-3,则S△BMH=$\frac{1}{2}$(t-3)2,
则S=4-$\frac{1}{2}$(4-t)2-$\frac{1}{2}$(t-3)2=-t2+7t-$\frac{17}{2}$;
当P在DE上时,PQ=2+(t-4)=t-2,
当MN在AB上时,$\frac{3}{2}$(t-2)=4,
解得:t=$\frac{14}{3}$.
当4<t≤$\frac{14}{3}$时,如图4.PC=2+(t-4)=t-2,CM=$\frac{3}{2}$(t-2).
BM=4-CM=4-$\frac{3}{2}$(t-2)=7-$\frac{3}{2}$t,
则S△BMH=$\frac{1}{2}$(7-$\frac{3}{2}$t)2=$\frac{1}{8}$(14-3t)2.
则S=4-$\frac{1}{8}$(14-3t)2=-$\frac{9}{8}$t2+$\frac{21}{2}$t-$\frac{41}{2}$;
当$\frac{14}{3}$<t≤6时,重合部分是S=S△OBC=4.
(4)过K作KG⊥NP于点G.如图5.
则PN'=$\frac{3}{2}$t,KG=t-1,PG=3-t,GN'=$\frac{3}{2}$t+t-3=$\frac{5}{2}$t-3.
当PK=KN'时,3-t=$\frac{5}{2}$t-3,
解得:t=$\frac{12}{7}$;
在直角△PKG中,PK2=(t-1)2+(3-t)2,
当PN'=PK时,(t-1)2+(3-t)2=($\frac{3}{2}$t)2,
解得:t=2$\sqrt{74}$-16或-2$\sqrt{74}$-16(舍去).
在直角△KN'G中,N'K2=($\frac{5}{2}$t-3)2+(t-1)2,
当N'K=PN'时,($\frac{5}{2}$t-3)2+(t-1)2=($\frac{3}{2}$t)2,
解得:t=$\frac{17+\sqrt{89}}{10}$(舍去)或$\frac{17-\sqrt{89}}{10}$.
总之,t=2$\sqrt{74}$-16或$\frac{12}{7}$或$\frac{17-\sqrt{89}}{10}$.
点评 本题考查了正方形的性质和等腰三角形的判定与性质,正确进行讨论是解决本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 比正数小的数一定都是负数 | |
| B. | 几个负数相加,和一定是负数 | |
| C. | 减去一个负数,等于加上一个非负数 | |
| D. | 两个负数相减,差一定是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
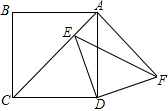 正方形ABCD边长为2$\sqrt{2}$,点E在对角线AC上,连接DE,将线段DE绕点D顺时针旋转90°至DF的位置,连接AF,EF.
正方形ABCD边长为2$\sqrt{2}$,点E在对角线AC上,连接DE,将线段DE绕点D顺时针旋转90°至DF的位置,连接AF,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
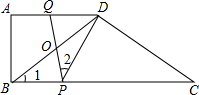 如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=DC,AB=6,AD=8,点P、Q分别为BC、AD上的动点,连接PQ,与BD相交于点O,
如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=DC,AB=6,AD=8,点P、Q分别为BC、AD上的动点,连接PQ,与BD相交于点O,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com