
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】对于一般的二次函数y=x2+bx+c,经过配方可化为y=(x﹣1)2+2,则b,c的值分别为( )
A.5,﹣1
B.2,3
C.﹣2,3
D.﹣2,﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式: ![]() =
= ![]() =1﹣
=1﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,…
,…
(1)由此可推导出 ![]() =;
=;
(2)猜想出能表示上述特点的一般规律,用含字母n的等式表示出来(n是正整数);
(3)请用(2)中的规律计算 ![]() +
+ ![]() +…+
+…+ ![]() 的结果.
的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE. 
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE. 
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由. 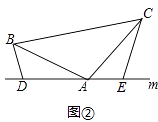
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com