
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
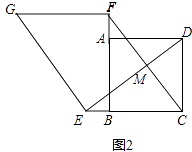
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;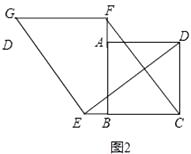
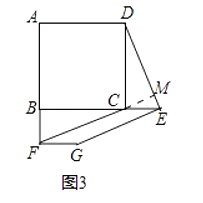
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.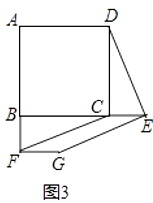
【答案】
(1)解:结论:FG=CE,FG∥CE.
理由:如图1中,设DE与CF交于点M.
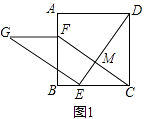
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
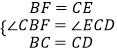 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
(2)解:结论仍然成立.
理由:如图2中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
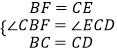 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
(3)解:结论仍然成立.
理由:如图3中,设DE与FC的延长线交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
∴∠CBF=∠DCE=90°
在△CBF和△DCE中,
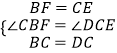 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
【解析】(1)结论:FG=CE,FG∥CE.如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(2)结论仍然成立.如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(3)结论仍然成立.如图3中,设DE与FC的延长线交于点M,证明方法类似.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y= ![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC. 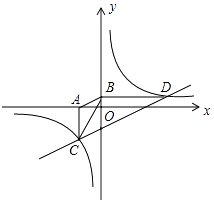
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式y1;
(3)根据图象直接写出y≥y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
次数 运动员 环数 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同学计算出了甲的成绩平均数是9,方差是![]() ,请作答:
,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙的射击成绩平均数都一样,则![]() ;
;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出![]() 的所有可能取值,并说明理由.
的所有可能取值,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,在![]() 中,
中,![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在点
落在点![]() 处.
处.
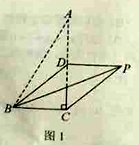
(1)如图1,若点![]() 是
是![]() 中点,连接
中点,连接![]() . ①写出
. ①写出![]() 的长;②求证:四边形
的长;②求证:四边形![]() 是平行四边形.
是平行四边形.
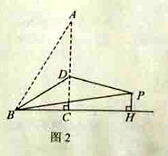
(2)如图2,若![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com