
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】
根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG;根据角的和差关系求得∠GAF=45°;在直角△ECG中,根据勾股定理可证CE=2DE;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;求出S△ECG,由S△FCG=![]() 即可得出结论.
即可得出结论.
①正确.理由:
∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴Rt△ABG≌Rt△AFG(HL);
②正确.理由:
∵∠BAG=∠FAG,∠DAE=∠FAE.
又∵∠BAD=90°,∴∠EAG=45°;
③正确.理由:
设DE=x,则EF=x,EC=12-x.在直角△ECG中,根据勾股定理,得:(12﹣x)2+62=(x+6)2,解得:x=4,∴DE=x=4,CE=12-x=8,∴CE=2DE;
④正确.理由:
∵CG=BG,BG=GF,∴CG=GF,∴∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GFC=2∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;

⑤正确.理由:
∵S△ECG=![]() GCCE=
GCCE=![]() ×6×8=24.
×6×8=24.
∵S△FCG=![]() =
=![]() =
=![]() .
.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).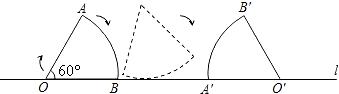
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
学习了无理数后,小航用这样的方法估算![]() 的近似值:
的近似值:
由于![]() ,不妨设
,不妨设![]() (
(![]() ),
),
所以![]() ,可得
,可得![]() .
.
由![]() 可知
可知![]() ,所以
,所以![]() ,
,
解得![]() , 则
, 则![]() .
.
依照小航的方法解决下列问题:
(1)估算![]() 的值.
的值.
(2)已知非负整数![]() 、
、![]() 、
、![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() .(用含
.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1: ![]() .
.
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 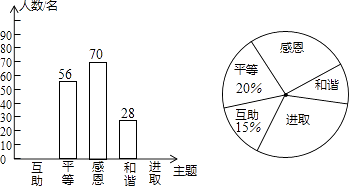
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点. 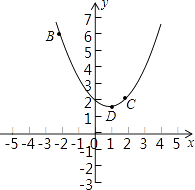
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线y=﹣ ![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上). 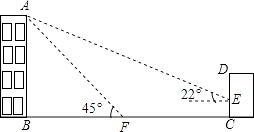
(参考数据:sin22°≈ ![]() ,cos22°
,cos22° ![]() ,tan22
,tan22 ![]() )
)
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
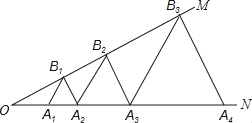
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com