

分析 (1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG,接下来在证明∠GAE=∠FAE,然后依据SAS证明△GAE≌△FAE即可;②由全等三角形的性质可知:AB=AH,GE=EF=5.设正方形的边长为x,接下来,在Rt△EFC中,依据勾股定理列方程求解即可;
(2)将△ABM逆时针旋转90°得△ADM′.在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2,接下来证明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′证明即可.
解答 解:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△GAE≌△FAE.
②∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x-2,FC=x-3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x-2)2+(x-3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.
(2)如图所示:将△ABM逆时针旋转90°得△ADM′.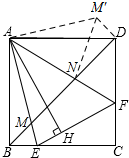
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,$\left\{\begin{array}{l}{AM=AM′}\\{∠MAN=M′AN}\\{AN=AN}\end{array}\right.$,
∴△AMN≌△ANM′.
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了旋转的性质、全等三角形的性质和判定、勾股定理的应用,正方形的性质,依据旋转的性质构造全等三角形和直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
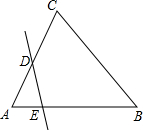 已知直线DE与不等边△ABC的两边AC,AB分别交于点D,E,若∠CAB=60°,则图中∠CDE+∠BED=( )
已知直线DE与不等边△ABC的两边AC,AB分别交于点D,E,若∠CAB=60°,则图中∠CDE+∠BED=( )| A. | 180° | B. | 210° | C. | 240° | D. | 270° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三条线段可以组成一个三角形 | B. | 400人中有两个人的生日在同一天 | ||
| C. | 早上的太阳从西方升起 | D. | 打开电视机,它正在播放动画片 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
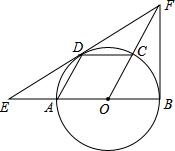 如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
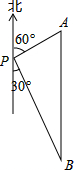 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )| A. | 60海里 | B. | 45海里 | C. | 20$\sqrt{3}$海里 | D. | 30$\sqrt{3}$海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com