
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $({x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}})({x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ | B. | $2({x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}})({x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ | ||
| C. | $2({x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}})({x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ | D. | $2({x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}})({x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
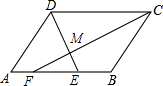 如图所示,?ABCD中,∠ADC和∠BCD的平分线交于点M,且分别交AB于E、F.
如图所示,?ABCD中,∠ADC和∠BCD的平分线交于点M,且分别交AB于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下,对称轴为直线x=-3 | B. | 顶点坐标为(-3,5) | ||
| C. | 最小值为5 | D. | 当x>3时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
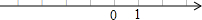 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
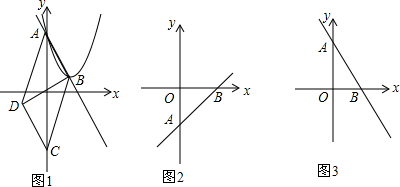
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
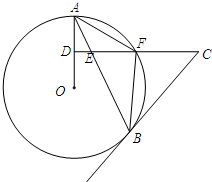 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com