
”¾ĢāÄæ”æČēĶ¼1£¬Į½øöČ«µČµÄ”÷ABCŗĶ”÷DEFÖŠ£¬”ĻACB=”ĻDFE=90”ć£¬AB=DE£¬ĘäÖŠµćBŗĶµćDÖŲŗĻ£¬µćFŌŚBCÉĻ£¬½«”÷DEFŃŲÉäĻßBCĘ½ŅĘ£¬ÉčĘ½ŅĘµÄ¾ąĄėĪŖx£¬Ę½ŅĘŗóµÄĶ¼ŠĪÓė”÷ABCÖŲŗĻ²æ·ÖµÄĆ껿ĪŖy£¬y¹ŲÓŚxµÄŗÆŹżĶ¼ĻóČēĶ¼2ĖłŹ¾£ØĘäÖŠ0”Üx”Üm£¬m£¼x”Ü3£¬3£¼x”Ü4Ź±£¬ŗÆŹżµÄ½āĪöŹ½²»Ķ¬£©
£Ø1£©ĢīæÕ£ŗBCµÄ³¤ĪŖ_____£»
£Ø2£©Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öxµÄȔֵ·¶Ī§£®

”¾“š°ø”æ£Ø1£©4£»£Ø2£©y= .
.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ
£Ø1£©½įŗĻĶ¼1”¢Ķ¼2·ÖĪöæÉÖŖ£¬µ±x=4Ź±£¬y=0£¬ĖµĆ÷“ĖŹ±£¬µćBŌĖ¶Æµ½ĮĖµćC£¬Į½Čż½ĒŠĪĪåÖŲµž²æ·Ö£¬“Ó¶ųæɵĆBC=4£»
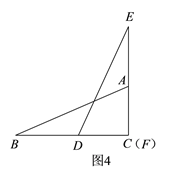
£Ø2£©·ÖĪöĶ¼1”¢Ķ¼2ÖŠµÄŠÅĻ¢æÉÖŖ£ŗµ±DE¾¹żµćAŹ±£ØČēĶ¼3£©£¬BD=x=3£¬CD=1£¬ĶعżÖ¤”÷ADC”×”÷BACæÉĒóµĆAC=2=DF£»·ÖĪöĶ¼1”¢Ķ¼2æÉÖŖµ±µćFÓėµćCÖŲŗĻŹ±£ØČēĶ¼4£©£¬BD=x=m=BC-DF=4-2=2£»ÕāŃłæÉµĆ£ŗČż¶ĪŗÆŹż¶ŌÓ¦µÄ×Ō±äĮæµÄȔֵ·¶Ī§·Ö±šŹĒ£ŗ¢Ł![]() £»¢Ś
£»¢Ś![]() £»¢Ū
£»¢Ū![]() £»°“ÕÕÕāČż¶Ī×Ō±äĮæµÄȔֵ·¶Ī§²ĪÕÕĶ¼5”¢Čē6”¢Ķ¼7½įŗĻŅŃÖŖĢõ¼ž·ÖĪö¼“æÉĒóµĆ¶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½£¬×īŗĆ×ŪŗĻ¼“æÉ.
£»°“ÕÕÕāČż¶Ī×Ō±äĮæµÄȔֵ·¶Ī§²ĪÕÕĶ¼5”¢Čē6”¢Ķ¼7½įŗĻŅŃÖŖĢõ¼ž·ÖĪö¼“æÉĒóµĆ¶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½£¬×īŗĆ×ŪŗĻ¼“æÉ.
ŹŌĢā½āĪö£ŗ
£Ø1£©ÓÉĶ¼2µĆµ±x=4Ź±£¬y=0£¬ĖµĆ÷“ĖŹ±”÷DEFÓė”÷ABCĪŽÖŲŗĻ²æ·Ö£¬
ŌņµćD“ÓBµ½CŌĖ¶ÆµÄ¾ąĄėĪŖ4£¬¼“BC=4£»
£Ø2£©ČēĶ¼3£¬µ±DE¾¹żµćAŹ±£¬ÓÉĶ¼2ÖŠµÄŠÅĻ¢æÉÖŖ£¬“ĖŹ±BD=x=3£¬CD=BC-BD=1£¬
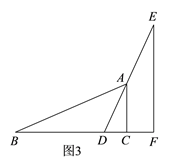
”ß”÷ABC”Õ”÷DEF£®
”ą”ĻEDF=”ĻBAC£®
”ß”ĻACD=”ĻBCA
”ą”÷ADC”×”÷BAC£®
”ą![]() £¬¼“
£¬¼“![]() £®½āµĆ£ŗAC=2£¬
£®½āµĆ£ŗAC=2£¬
”ąDF=AC=2.
·ÖĪöĶ¼1”¢Ķ¼2æÉÖŖµ±µćFÓėµćCÖŲŗĻŹ±£ØČēĶ¼4£©£¬BD=x=m=BC-DF=4-2=2.
”ąČż¶ĪŗÆŹż¶ŌÓ¦µÄ×Ō±äĮæµÄȔֵ·¶Ī§·Ö±šŹĒ£ŗ¢Ł![]() £»¢Ś
£»¢Ś![]() £»¢Ū
£»¢Ū![]() £»
£»
¢Łµ±0”Üx”Ü2Ź±£ØČēĶ¼5£©£¬
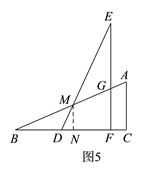
ÉčED”¢EFÓėAB·Ö±šĻą½»ÓŚµćM£¬G£¬×÷MN”ĶBC£¬“¹×ćĪŖN£®
Ōņ”ĻMNB=90”ć=”ĻEFD=”ĻC£®
”ß”ĻMDN=”ĻEDF£®
”ą”÷DMN”×”÷DEF£®
”ą![]() £¬¼“
£¬¼“![]() £®
£®
”ąMN=2DN£®
ÉčDN=n£¬ŌņMN=2n£®
Ķ¬Ąķ”÷BMN”×”÷BAC£®
”ą![]() £®¼“
£®¼“![]() £¬
£¬
”ąBN=4n£¬¼“x+n=4n£®
”ąn=![]() x£®
x£®
”ąS”÷BDM=![]() BDMN=
BDMN=![]()
Ķ¬Ąķ”÷BGF”×”÷BAC
”ą![]() £¬¼“
£¬¼“![]() £®
£®
”ąGF=![]() (x+2)£¬
(x+2)£¬
”ąy=S”÷BGF©S”÷BDM=![]() £Øx+2£©”Į
£Øx+2£©”Į![]() £Øx+2£©-
£Øx+2£©-![]() =©
=©![]() x2+x+1£®
x2+x+1£®
¢Śµ±2£¼x”Ü3Ź±£ØČēĶ¼6£©£¬
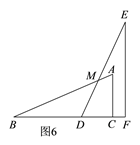
ÓÉ¢ŁÖŖ£¬S”÷BDM=![]() x2£®
x2£®
”ąy=S”÷ABC©S”÷BDM=![]() ”Į2”Į4-
”Į2”Į4-![]() x2=©
x2=©![]() x2+4
x2+4
¢Ūµ±3£¼x”Ü4Ź±£ØČēĶ¼7£©£¬
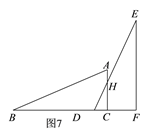
ÉčDEÓėABĻą½»ÓŚµćH£¬Ōņ£ŗ”÷DHC”×”÷DEF£®
”ą![]() £¬¼“
£¬¼“![]()
”ąHC=24©x£®
”ąy=![]() =x2©8x+16£¬
=x2©8x+16£¬
×ŪÉĻĖłŹö£¬æɵĆy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
y= £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪOABCµÄĮ½±ßOA”¢OC·Ö±šŌŚxÖį”¢yÖįÉĻ£¬µćD£Ø5£¬3£©ŌŚ±ßABÉĻ£¬ŅŌCĪŖÖŠŠÄ£¬°Ń”÷CDBŠż×Ŗ90”ć£¬ŌņŠż×ŖŗóµćDµÄ¶ŌÓ¦µćD”äµÄ×ų±źŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬EŹĒ±ßABÉĻµÄŅ»¶Æµć£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬Į¬½ÓDE£¬µćA¹ŲÓŚÖ±ĻßDEµÄ¶Ō³ĘµćĪŖF£¬Į¬½ÓEF²¢ŃÓ³¤½»BCÓŚµćG£¬Į¬½ÓDG£¬¹żµćE×÷EH”ĶDE½»DGµÄŃÓ³¤ĻßÓŚµćH£¬Į¬½ÓBH£®
£Ø1£©ĒóÖ¤£ŗGF=GC£»
£Ø2£©ÓƵȏ½±ķŹ¾Ļ߶ĪBHÓėAEµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆĪŽæĢ¶ČÖ±³ß×÷Ķ¼²¢½ā“šĪŹĢā£ŗ
ČēĶ¼£¬![]() ŗĶ
ŗĶ![]() ¶¼ŹĒµČ±ßČż½ĒŠĪ£¬ŌŚ
¶¼ŹĒµČ±ßČż½ĒŠĪ£¬ŌŚ![]() ÄŚ²æ×öŅ»µć
ÄŚ²æ×öŅ»µć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() £¬²¢øųÓčÖ¤Ć÷£®
£¬²¢øųÓčÖ¤Ć÷£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćB£Øa£¬b£©ŌŚµŚŅ»ĻóĻŽ£¬¹żB×÷BA”ĶyÖįÓŚA£¬¹żB×÷BC”ĶxÖįÓŚC£¬ĒŅŹµŹża”¢bĀś×ć£Øa-b-2£©2+|2a+b-10|”Ü0£¬ŗ¬45½ĒµÄRt”÷DEFµÄŅ»ĢõÖ±½Ē±ßDFÓėxÖįÖŲŗĻ£¬DE”ĶxÖįÓŚD£¬µćFÓė×ų±źŌµćÖŲŗĻ£¬DE=DF=3£®”÷DEF“ÓijŹ±æĢæŖŹ¼ŃŲ×Å×ų±źÖįŅŌ1øöµ„Ī»³¤¶ČĆæĆėµÄĖŁ¶ČŌČĖŁŌĖ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©ĒóµćBµÄ×ų±ź£»
£Ø2£©Čō”÷DEFŃŲ×ÅyÖįøŗ·½ĻņŌĖ¶Æ£¬Į¬½ÓAE£¬EGĘ½·Ö”ĻAEF£¬EHĘ½·Ö”ĻAED£¬µ±EG”ĪDFŹ±£¬Ēó”ĻHEFµÄ¶ČŹż£»
£Ø3£©Čō”÷DEFŃŲ×ÅxÖįÕż·½ĻņŌĖ¶Æ£¬ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬¼Ē”÷AEFÓė³¤·½ŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£¬µ±0£¼t”Ü4£¬S=![]() Ź±£¬ĒėÄćĒó³öŌĖ¶ÆŹ±¼ät£®
Ź±£¬ĒėÄćĒó³öŌĖ¶ÆŹ±¼ät£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µČŃüÖ±½ĒČż½ĒŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬
ÖįÉĻ£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬
£¬![]() ½»
½»![]() ÖįÓŚ
ÖįÓŚ![]() £¬
£¬

£Ø1£©Ēóµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø2£©Į¬½Ó![]() £¬Ēó
£¬Ēó![]() µÄĆ껿£»
µÄĆ껿£»
£Ø3£©ŌŚ![]() ÖįÉĻÓŠŅ»¶Æµć
ÖįÉĻÓŠŅ»¶Æµć![]() £¬µ±
£¬µ±![]() µÄÖµ×īŠ”Ź±£¬Ēó“ĖŹ±
µÄÖµ×īŠ”Ź±£¬Ēó“ĖŹ±![]() µÄ×ų±ź£®
µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬
ÉĻ£¬![]() ÓŚµć
ÓŚµć![]() £¬
£¬![]() µÄŃÓ³¤Ļß½»
µÄŃÓ³¤Ļß½»![]() µÄŃÓ³¤ĻßÓŚµć
µÄŃÓ³¤ĻßÓŚµć![]() £¬ŌņĻĀĮŠ½įĀŪÖŠ“ķĪóµÄŹĒ£Ø £©
£¬ŌņĻĀĮŠ½įĀŪÖŠ“ķĪóµÄŹĒ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ŗģŗĶŠ”Ć÷ŌŚ²Ł³”×öÓĪĻ·£¬ĖūĆĒĻČŌŚµŲÉĻ»ĮĖ°ė¾¶·Ö±š2mŗĶ3mµÄĶ¬ŠÄŌ²£ØČēĶ¼£©£¬ĆÉÉĻŃŪŌŚŅ»¶Ø¾ąĄėĶāĻņȦČ֥Š”ŹÆ×Ó£¬ÖĄÖŠŅõÓ°Š”ŗģŹ¤£¬·ńŌņŠ”Ć÷Ź¤£¬Ī“ÖĄČėȦČ²»Ėć£¬Ä楓µ±²ĆÅŠ£®
£Ø1£©ÄćČĻĪŖÓĪĻ·¹«Ę½Āš£æĪŖŹ²Ć“£æ
£Ø2£©ÓĪĻ·½įŹų£¬Š”Ć÷±ß×ß±ßĻė£¬”°·“¹żĄ“£¬ÄÜ·ńÓĆʵĀŹ¹Ą¼ĘøÅĀŹµÄ·½·Ø£¬Ą“¹ĄĖćijŅ»²»¹ęŌņĶ¼ŠĪµÄĆ껿ÄŲ”±£®ĒėÄćÉč¼Ę·½°ø£¬½ā¾öÕāŅ»ĪŹĢā£®£ØŅŖĒó²¹³äĶźÕūĶ¼ŠĪ£¬ĖµĆ÷Éč¼Ę²½Öč”¢ŌĄķ£¬Š“³ö¹ĄĖć¹«Ź½£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹŠÕž¹«Ė¾ĪŖĀĢ»Æ½ØÉčĀ··ē¾°“ų£¬¼Ę»®¹ŗĀņ¼×ŅŅĮ½ÖÖŹ÷Ćē600Öź£¬¼×ÖÖŹ÷ĆēĆæÖź50ŌŖ£¬ŅŅÖÖŹ÷ĆēĆæÖź70ŌŖ£®ÓŠ¹ŲĶ³¼Ę±ķĆ÷£¬¼×ŅŅĮ½ÖÖŹ÷ĆēµÄ³É»īĀŹ·Ö±šĪŖ80%ŗĶ95%£®£Ø×¢£ŗ³É»īĀŹ=![]() ”Į100%£©£®
”Į100%£©£®
£Ø1£©Čō¹ŗĀņŹ÷ĆēµÄĒ®²»³¬¹ż40000ŌŖ£¬Ó¦ČēŗĪŃ”¹ŗ¼×”¢ŅŅĮ½ÖÖŹ÷Ćē£»
£Ø2£©ČōĻ£ĶūÕāÅśŹ÷ĆēµÄ³É»īĀŹ²»µĶÓŚ90%£¬ĒŅ¹ŗĀņŹ÷ĆēµÄ·ŃÓĆ×īµĶ£¬Ó¦ČēŗĪŃ”¹ŗ¼×”¢ŅŅĮ½ÖÖŹ÷Ćē²¢Ēó³ö×īµĶ·ŃÓĆŹĒ¶ąÉŁŌŖ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com