
 已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).
已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).分析 (1)令抛物线l1:y=0,可求得点A和点B的坐标,然后设设抛物线l2的解析式为y=a(x+1)(x-4),将点D的坐标代入可求得a的值,从而得到抛物线的解析式;
(2)①由点A和点B的坐标可求得AB的长,设P(x,0),则M(x,-x2+2x+3),N(x,$\frac{1}{2}$x2-$\frac{3}{2}$x-2).然后依据SAMBN=$\frac{1}{2}$AB•MN列出S与x的函数关系,从而可得到当S有最大值时,x的值,于是可得到点P的坐标;②CM与DN不平行时,可证明四边形CDNM为等腰梯形,然后可证明GM=HN,设P(x,0),则M(x,-x2+2x+3),N(x,$\frac{1}{2}$x2-$\frac{3}{2}$x-2).从而可列出关于x的方程,于是可求得点P的坐标;当CM∥DN时,四边形CDNM为平行四边形.故此DC=MN=5,从而得到关于x的方程,从而可求得点P的坐标.
解答 解:(1)∵令-x2+2x+3=0,解得:x1=-1,x2=3,
∴A(-1,0),B(3,0).
设抛物线l2的解析式为y=a(x+1)(x-4).
∵将D(0,-2)代入得:-4a=-2,
∴a=$\frac{1}{2}$.
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)①如图1所示: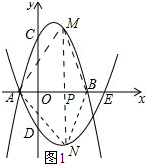
∵A(-1,0),B(3,0),
∴AB=4.
设P(x,0),则M(x,-x2+2x+3),N(x,$\frac{1}{2}$x2-$\frac{3}{2}$x-2).
∵MN⊥AB,
∴SAMBN=$\frac{1}{2}$AB•MN=-3x2+7x+10(-1<x<3).
∴当x=$\frac{7}{6}$时,SAMBN有最大值.
∴此时P的坐标为($\frac{7}{6}$,0).
②如图2所示:作CG⊥MN于G,DH⊥MN于H,如果CM与DN不平行.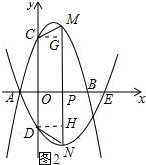
∵DC∥MN,CM=DN,
∴四边形CDNM为等腰梯形.
∴∠DNH=∠CMG.
在△CGM和△DNH中$\left\{\begin{array}{l}{∠DNH=∠CMG}\\{∠DHN=∠CGM}\\{DN=CM}\end{array}\right.$,
∴△CGM≌△DNH.
∴MG=HN.
∴PM-PN=1.
设P(x,0),则M(x,-x2+2x+3),N(x,$\frac{1}{2}$x2-$\frac{3}{2}$x-2).
∴(-x2+2x+3)+($\frac{1}{2}$x2-$\frac{3}{2}$x-2)=1,解得:x1=0(舍去),x2=1.
∴P(1,0).
当CM∥DN时,如图3所示:
∵DC∥MN,CM∥DN,
∴四边形CDNM为平行四边形.
∴DC=MN.=5
∴-x2+2x+3-($\frac{1}{2}$x2-$\frac{3}{2}$x-2)=5,
∴x1=0(舍去),x2=$\frac{7}{3}$,
∴P($\frac{7}{3}$,0).
总上所述P点坐标为(1,0),或($\frac{7}{3}$,0).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、等腰梯形的性质、全等三角形的性质、平行四边形的性质和判定,依MN=DC=5、PM-PN=1列出关于P的横坐标x的方程是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
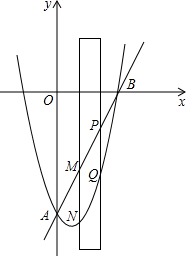 如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).
如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°
(1)计算:|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com