
分析 (1)直接计算,写成幂的形式即可;
(2)利用(1)中所示的规律能推断出n个从1开始的连续奇数之和等于n2;
(3)将原式变形为1+3+…+25+27+29+31+…+185-(1+3+…+25),再利用(2)中规律计算可得.
解答 解:(1)1=1=12,
1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
1+3+5+7+9+11=36=62,
故答案为:1、2、3、4、5、6;
(2)由(1)知,$\underset{\underbrace{1+3+5+7+…+(2n-1)^{2}}}{n个连续奇数}$=n2,
故答案为:n;
(3)原式=1+3+…+25+27+29+31+…+185-(1+3+…+25)
=932-132
=(93+13)×(93-13)
=8480.
点评 本题主要考查数字的变化规律,根据题意得出n个从1开始的连续奇数之和等于n2是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
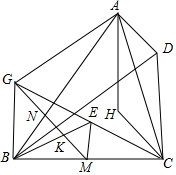 如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.
如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com