
����Ŀ���ܺ���Ӱ�죬�Ա����ϵĵ���ȡů�����ۻ�����ij��������ÿ̨�ɱ��۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȡů�����±��ǽ���������������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȡů�������۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȡů����30̨����A���ͺŵĵ���ȡů������ܲɹ�����̨��
���𰸡�
��1���⣺��A��B�����ͺŵĵ���ȡů�������ۼ۷ֱ�Ϊx��yԪ��
�� ![]() ��
��
��ã� ![]() ��
��
��A��B�����ͺŵ���ȡů�������۽�ֱ�Ϊ250Ԫ��210Ԫ��
��2���⣺��ɹ�A���ͺŵ���ȡů��ą����ɹ�B���ͺŵĵ���ȡů����30��a��̨��
��200a+170��30��a����5400��
��ã�a��10��
�����ɹ�A���ͺŵĵ����10̨��
����������1����A��B�����ͺŵĵ���ȡů�������ۼ۷ֱ�Ϊx��yԪ������3̨A���ͺź�5̨B���ͺŵĵ���ȡů������1800Ԫ��4̨A���ͺź�10̨B���ͺŵĵ���ȡů������3100Ԫ���г���������⼴�ɣ���2����ɹ�A���ͺŵ���ȡů��ą����ɹ�B���ͺŵĵ���ȡů����30��a��̨�����ݽ�����5400Ԫ���г�����ʽ��⼴��.


 ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺[��x+y��2����x��y��2]�£�2xy����
��2���ⷽ�̣�![]()
��3����ʽ�ֽ⣺xy2��4x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ʒԭ���ĵ��ۺ�Ϊ100Ԫ�����г��仯������Ʒ����10%������Ʒ���40%�����ۺ�������Ʒ�ĵ��ۺͱ�ԭ���ĵ��ۺ������20%���ס���������Ʒԭ���ĵ��۸��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˷���ʽ��̽����Ӧ�ã�
��ѧ�����,��ʦ�������ɸ���ͼ1������ֽƬ��A��ֽƬ�߳�Ϊ![]() �������Σ�B��ֽƬ�DZ߳�Ϊ
�������Σ�B��ֽƬ�DZ߳�Ϊ![]() �������Σ�C��ֽƬ��Ϊ
�������Σ�C��ֽƬ��Ϊ![]() ��Ϊ
��Ϊ![]() �ij����Σ�����A��ֽƬһ�ţ�B��ֽƬһ�ţ�C��ֽƬ����ƴ����ͼ2�Ĵ������Ρ�
�ij����Σ�����A��ֽƬһ�ţ�B��ֽƬһ�ţ�C��ֽƬ����ƴ����ͼ2�Ĵ������Ρ�
(1)�������ֲ�ͬ�ķ�����ʾͼ2�������ε������
����1:_____________________������2:_____________________.
(2)�۲�ͼ2,����д��������������ʽ:![]() ֮��ĵ�����ϵ��
֮��ĵ�����ϵ��
(3)���Ƶ�,������ͼ1�е�����ֽƬƴһ��ͼ����֤:![]()
(4)����(2)���еĵ�����ϵ,�����������:
��֪:![]() ��
��![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������쳧������һ����ʽ�綯�������ƻ�һ��������װ240�������ڳ�������㹻���������������ʽ�綯�����İ�װ,����������ƸһЩ�¹���:���Ǿ�����ѵ���ϸ�,Ҳ�ܶ������е綯�����İ�װ��������ʼ��,���в��ŷ���:1����������2���¹���ÿ�¿ɰ�װ8���綯������2����������3���¹���ÿ�¿ɰ�װ14���綯������
(1)ÿ�����������¹���ÿ�·ֱ����װ�������綯������
(2)���������Ƹ�¹���������(�¹�����������10��)�ͳ��������������,�պ������һ��İ�װ����,��ô�������ļ����¹��˵���Ƹ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD��һ��Ա�AD��BC���ӳ��߽��ڵ�E��
��1����ͼ1������ABC=��ADC=90�㣬��֤��EDEA=ECEB��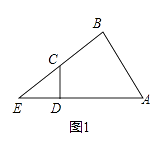
��2����ͼ2������ABC=120�㣬cos��ADC= ![]() ��CD=5��AB=12����CDE�����Ϊ6�����ı���ABCD�������
��CD=5��AB=12����CDE�����Ϊ6�����ı���ABCD�������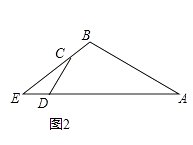
��3����ͼ3����һ��Ա�AB��DC���ӳ����ཻ�ڵ�F����cos��ABC=cos��ADC= ![]() ��CD=5��CF=ED=n��ֱ��д��AD�ij����ú�n��ʽ�ӱ�ʾ��
��CD=5��CF=ED=n��ֱ��д��AD�ij����ú�n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻͬѧ�ǵĿ������ijУ���������꼶ѧ���п�չ��������ƹ�����Լ���ë������������������Ҫ��ÿ��ѧ��������ֻ��ѡ������һ��![]() Ϊ����ǰ�˽�ѡ�����������Ŀ��ѧ����������ΪУѧ����������������Сǿ�������ȡ�˲������꼶ѧ�������ʾ����飬�����Ƴ�������������������ͳ��ͼ
Ϊ����ǰ�˽�ѡ�����������Ŀ��ѧ����������ΪУѧ����������������Сǿ�������ȡ�˲������꼶ѧ�������ʾ����飬�����Ƴ�������������������ͳ��ͼ![]() �����ͳ��ͼ�ش���������
�����ͳ��ͼ�ش���������
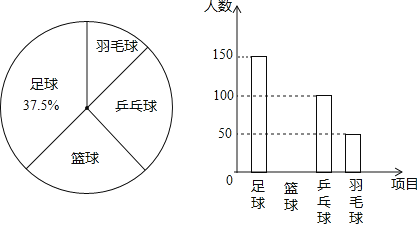
![]() �����ʾ������ѧ���ж����ˣ�����ȫ����ͳ��ͼ��
�����ʾ������ѧ���ж����ˣ�����ȫ����ͳ��ͼ��
![]() ������ͳ��ͼ�У�ѡ��ƹ������Ŀ�����ε�Բ�Ľ��Ƕ��ٶȣ�
������ͳ��ͼ�У�ѡ��ƹ������Ŀ�����ε�Բ�Ľ��Ƕ��ٶȣ�
![]() ����У���꼶������Ϊ1200�ˣ������ѡ����ë����Ŀ������һ���Ƕ����ˣ�
����У���꼶������Ϊ1200�ˣ������ѡ����ë����Ŀ������һ���Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��y�ύ�ڵ�A����x�ύ�ڵ�B����A�������ꡢ��B�ĺ�������ͼ��ʾ��
(1)��ֱ��AB��Ӧ�ĺ�������ʽ��
(2)��P��ֱ��AB�ϣ��Ƿ���ڵ�Pʹ��������AOP�����Ϊ1��������ڣ�����������������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����Ҫ����ѧУʳ�ú�ʳ����ǰ��һ�����ĸ߶ȣ�����ʳ��¥��M����������ǰ��3����A�������������E������Ϊ30�㣬���ּ�������̨����C����������Ķ���E��������60�㣬�ټ�����ǰ�ߵ�������D�������ʳ��¥��N������Ϊ45�㣮��֪A�������ĸ߶�AB=2�ף���BCA=30�㣬��B��C��D������ͬһֱ���ϣ�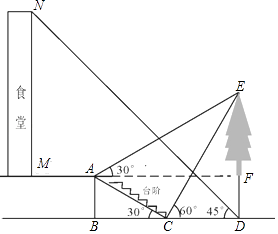
��1������DE�ĸ߶ȣ�
��2����ʳ��MN�ĸ߶ȣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com