
 (1)已知∠AOB=30°,∠BOC=45°,则∠AOC等于15°或75°.
(1)已知∠AOB=30°,∠BOC=45°,则∠AOC等于15°或75°.分析 (1)分为两种情况,利当∠AOB在∠BOC的内部时,当∠AOB在∠BOC的外部时,再求出即可;
(2)先求出∠AOC,根据角平分线定义求出∠EOC和∠DOC,再求出即可.
解答 解:(1)此题要分情况:
当∠AOB在∠BOC的内部时,∠AOC=∠BOC-∠AOB=15°;
当∠AOB在∠BOC的外部时,∠AOC=∠BOC+∠AOB=75°.
故答案为:15°或75°;
(2)∵∠BOC=60°,
∴∠AOC=180°-∠BOC=120°,
∵OE,OD分别为∠AOC和∠BOC的平分线,
∴∠COE=$\frac{1}{2}$∠AOC=60°,∠DOC=$\frac{1}{2}$∠BCO=30°,
∴∠EOD=∠EOC+∠DOC=90°,
故答案为:90°.
点评 本题考查了角的有关计算和角平分线定义的应用,能求出各个角的度数是解此题的关键,此类题由于没有图形,所以要分情况讨论.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
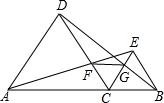 已知:如图,A、C、B在同一直线上,△ADC和△BCE都是正三角形,DB、EA分别交CE、DC于G、F.求证:
已知:如图,A、C、B在同一直线上,△ADC和△BCE都是正三角形,DB、EA分别交CE、DC于G、F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
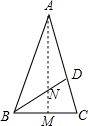 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )| A. | ∠BAC=36° | |
| B. | BD平分∠ABC | |
| C. | 若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54° | |
| D. | 点N是BD的中点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )| A. | 225 | B. | 63 | C. | 50 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
在平面直角坐标系中,△ABC的三个顶点的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com