
【题目】一个三角形的三边长分别为15,20和25,那么它的最长边上的高为( ).
A. 12.5B. 12C. ![]() D. 9
D. 9
科目:初中数学 来源: 题型:
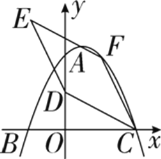
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
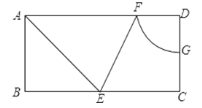
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,则![]() 的长为________
的长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
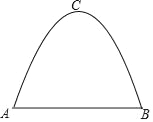
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
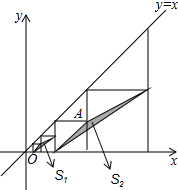
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com