
(满分l4分)如图,点P是双曲线y= (k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=
(k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=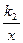 (0<k2<︱k1︱)于E,F两点.
(0<k2<︱k1︱)于E,F两点.
(1)图①中,四边形PEOF 的面积S1=__________(用含k1,k2的式子表示);
(2)图②中,设点P坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记S2=S△PEF-S△OEF,S2是否有最小值?若有,求出其最小值;若没有,请说明理由
解:(1)k2+k1; ……3分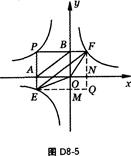
(2)OEF∥AB. ……4分
证明:如图D8—5,由题得A(-4,0),B(0,3),
E(-4,-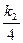 ),F(
),F(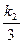 ,3).
,3).
∴PA=3,PE=3+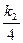 ,PB=4,PF=4+
,PB=4,PF=4+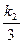 .
.
∴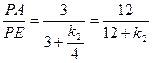 ,
,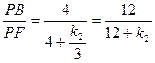
∴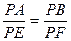 ……7分
……7分
又∵∠APB=∠EPF.
∴△APB∽△EPF.∴∠PAB=∠PEF.
∴EF∥AB. ……8分
②S2没有最小值,理由如下:
过点E作EM⊥y轴于点M,过点F作FN⊥x轴于点N,两线交于点Q.
由上知M(0,-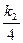 ),N(
),N(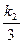 ,0),Q(
,0),Q(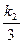 ,-
,-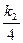 ). ……10分
). ……10分
而S△EFQ=S△PEF,
∴S2=S△PEF一S△OEF=S△EFQ一S△OEF=S△EOM+S△FON+S矩行OMQN
=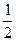 k2+
k2+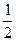 k2+
k2+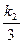 ·
·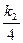
= k2+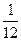 k22
k22
= 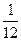 (k2+6) 2—3. ……12分
(k2+6) 2—3. ……12分
当k2>一6时,S2的值随k2的增大而增大,而0<k2<12. ……13分
∴O<S2<24,S2没有最小值. ……l4分
解析


科目:初中数学 来源: 题型:
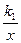 (k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=
(k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=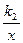 (0<k2<︱k1︱)于E,F两点.
(0<k2<︱k1︱)于E,F两点.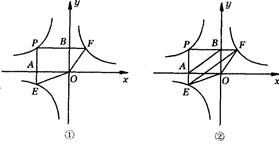
查看答案和解析>>
科目:初中数学 来源: 题型:
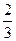 x+
x+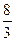 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.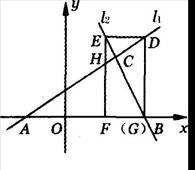
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2010年浙江省初中毕业生学业考试模拟试卷数学卷 题型:解答题
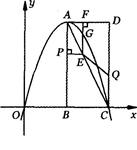
(满分l4分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8).抛物线y=ax2+bx过A,C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,过点E作EF上AD交AD于点F,交抛物线于点G.当t为何值时,线段EG最长?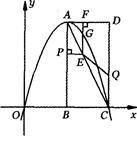
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com