
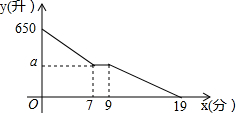
 某公司一辆绿化洒水车以每分50升的速度给一片树林浇水,一段时间后关闭洒水阀门,行驶到一片草坪处,以另一洒水速度匀速给草坪浇水,直到洒水车内的水全部用光,洒水车内的水量y(升)与时间x(分)之间的函数图象如图所示.
某公司一辆绿化洒水车以每分50升的速度给一片树林浇水,一段时间后关闭洒水阀门,行驶到一片草坪处,以另一洒水速度匀速给草坪浇水,直到洒水车内的水全部用光,洒水车内的水量y(升)与时间x(分)之间的函数图象如图所示.分析 (1)根据总量=每分钟浇水量×浇水时间,即可求出洒水车给树林浇水总量,用650-浇水总量即可求出a值;
(2)设洒水车给草坪浇水时y与x之间的函数关系式为y=kx+b(k≠0),根据点的坐标,利用待定系数法即可求出y与x之间的函数关系式;
(3)将x=13代入(2)结论中求出y值,用650减去剩余水量即可得出结论.
解答 解:(1)洒水车给树林浇水总量为50×7=350(升),
a=650-350=300(升).
答:a的值为300.
(2)设洒水车给草坪浇水时y与x之间的函数关系式为y=kx+b(k≠0),
将点(9,300)、(19,0)代入y=kx+b,
得:$\left\{\begin{array}{l}{9k+b=300}\\{19k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-30}\\{b=570}\end{array}\right.$.
∴洒水车给草坪浇水时y与x之间的函数关系式为y=-30x+570(9≤x≤19).
(3)当x=13时,y=-30x+570=180,
∴650-180=470(升).
答:当x=13时,洒水车共浇水470升.
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,解题的关键是:(1)根据总量=每分钟浇水量×浇水时间,求出洒水车给树林浇水总量;(2)根据点的坐标,利用待定系数法求出一次函数关系式;(3)利用一次函数图象上点的坐标特征,求出当x=13时洒水车剩余水量.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:选择题
| A. | 52016-1 | B. | 52017-1 | C. | $\frac{{{5^{2016}}-1}}{4}$ | D. | $\frac{{{5^{2017}}-1}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
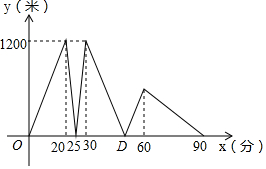 某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C;乙在甲出发20分钟后乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C:甲、乙两人同时到达景点C,甲、乙两人之间的距离y(米)与甲出发的时间x(分)之间的函数图象如图所示.
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C;乙在甲出发20分钟后乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C:甲、乙两人同时到达景点C,甲、乙两人之间的距离y(米)与甲出发的时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$都是无理数 | |
| B. | 无理数包括正无理数,零和负无理数 | |
| C. | 无理数是开方开不尽的数 | |
| D. | 数轴上的每一个点都表示一个实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com