
����Ŀ����ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E�� 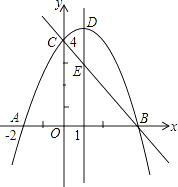
��1���������ߵĽ���ʽ��
��2������F��ֱ��BC�Ϸ����������ϵ�һ�����㣬�Ƿ���ڵ�Fʹ�ı���ABFC�����Ϊ17�������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮
���𰸡�
��1���⣺��������y=ax2+bx+c��a��0������C��0��4����
��c=4 �٣�
�߶Գ���x=�� ![]() =1��
=1��
��b=��2a �ڣ�
�������߹���A����2��0����
��0=4a��2b+c �ۣ�
�ɢ٢ڢ۽�ã�a=�� ![]() ��b=1��c=4��
��b=1��c=4��
�������ߵĽ���ʽΪy=�� ![]() x2+x+4
x2+x+4
��2���⣺����һ������������������ĵ�F����ͼ��ʾ������BF��CF��OF������F��FH��x���ڵ�H��FG��y���ڵ�G��
���F��������t���� ![]() t2+t+4��������0��t��4��
t2+t+4��������0��t��4��
��FH=�� ![]() t2+t+4��FG=t��
t2+t+4��FG=t��
��S��OBF= ![]() OBFH=
OBFH= ![]() ��4������
��4������ ![]() t2+t+4��=��t2+2t+8��
t2+t+4��=��t2+2t+8��
S��OFC= ![]() OCFG=
OCFG= ![]() ��4��t=2t��
��4��t=2t��
��S�ı���ABFC=S��AOC+S��OBF+S��OFC=4��t2+2t+8+2t=��t2+4t+12��
�t2+4t+12=17��
��t2��4t+5=0��
���=����4��2��4��5=��4��0��
���t2��4t+5=0�⣬
�ʲ��������������ĵ�F
��������
��B��4��0����C��0��4����
��lBC��y=��x+4��
��F����x�ᴹ�ߣ���BC��H����F��t���� ![]() t2+t+4����
t2+t+4����
��H��t����t+4����
��S�ı���ABFC=S��ABC+S��BCF=17��
�� ![]() ��4+2����4+
��4+2����4+ ![]() ����
���� ![]() t2+t+4+t��4����4=17��
t2+t+4+t��4����4=17��
��t2��4t+5=0��
���=����4��2��4��5��0��
���t2��4t+5=0�⣬�ʲ��������������ĵ�F
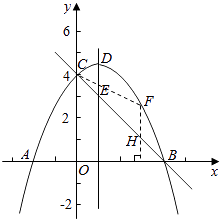
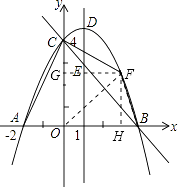
��3���⣺����һ����ֱ��BC�Ľ���ʽΪy=kx+n��k��0����
��B��4��0����C��0��4����
�� ![]() ��
��
��� ![]() ��
��
��ֱ��BC�Ľ���ʽΪy=��x+4��
��y=�� ![]() x2+x+4=��
x2+x+4=�� ![]() ��x��1��2+
��x��1��2+ ![]() ��
��
�ඥ��D��1�� ![]() ����
����
�ֵ�E��ֱ��BC�ϣ����E��1��3����
����DE= ![]() ��3=
��3= ![]() ��
��
����D��E��P��QΪ������ı�����ƽ���ı��Σ���ΪDE��PQ��ֻ��DE=PQ��
���P�������ǣ�m����m+4�������Q�������ǣ�m���� ![]() m2+m+4����
m2+m+4����
�� ��0��m��4ʱ��PQ=���� ![]() m2+m+4��������m+4��=��
m2+m+4��������m+4��=�� ![]() m2+2m��
m2+2m��
�ɩ� ![]() m2+2m=
m2+2m= ![]() ��
��
��ã�m=1��3��
��m=1ʱ���߶�PQ��DE�غϣ�m=1��ȥ��
��m=3��P1��3��1����
�ڵ�m��0��m��4ʱ��PQ=����m+4�������� ![]() m2+m+4��=
m2+m+4��= ![]() m2��2m��
m2��2m��
�� ![]() m2��2m=
m2��2m= ![]() ��
��
���m=2�� ![]() ���������ʺ����⣬
���������ʺ����⣬
��ʱP2��2+ ![]() ��2��
��2�� ![]() ����P3��2��
����P3��2�� ![]() ��2+
��2+ ![]() ����
����
������������������ĵ�P���������ֱ���P1��3��1����P2��2+ ![]() ��2��
��2�� ![]() ����P3��2��
����P3��2�� ![]() ��2+
��2+ ![]() ��
��
��������
��DE��PQ��
�൱DE=PQʱ����D��E��P��QΪ������ı�����ƽ���ı��Σ�
��y=�� ![]() x2+x+4��
x2+x+4��
��D��1�� ![]() ����
����
��lBC��y=��x+4��
��E��1��3����
��DE= ![]() ��3=
��3= ![]() ��
��
���F�������ǣ�m����m+4�������Q�������ǣ�m���� ![]() m2+m+4����
m2+m+4����
��|��m+4+ ![]() m2��m��4|=
m2��m��4|= ![]() ��
��
�� ![]() m2��2m=
m2��2m= ![]() ��
�� ![]() m2��2m=��
m2��2m=�� ![]() ��
��
��m=1��m=3��m=2+ ![]() ��m=2��
��m=2�� ![]() ��
��
�����飬��m=1ʱ���߶�PQ��DE�غϣ�����ȥ��
��P1��3��1����P2��2+ ![]() ��2��
��2�� ![]() ����P3��2��
����P3��2�� ![]() ��2+
��2+ ![]() ����
����
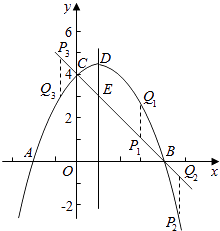
������������һ����1���Ȱ�C��0��4������y=ax2+bx+c���ó�c=4�٣����������ߵĶԳ���x=�� ![]() =1���õ�b=��2a�ڣ������߹���A����2��0�����õ�0=4a��2b+c�ۣ�Ȼ���ɢ٢ڢۿɽ�ã�a=��
=1���õ�b=��2a�ڣ������߹���A����2��0�����õ�0=4a��2b+c�ۣ�Ȼ���ɢ٢ڢۿɽ�ã�a=�� ![]() ��b=1��c=4��������������ߵĽ���ʽΪy=��
��b=1��c=4��������������ߵĽ���ʽΪy=�� ![]() x2+x+4����2������������������ĵ�F������BF��CF��OF������F��FH��x���ڵ�H��FG��y���ڵ�G�����F������Ϊ��t����
x2+x+4����2������������������ĵ�F������BF��CF��OF������F��FH��x���ڵ�H��FG��y���ڵ�G�����F������Ϊ��t���� ![]() t2+t+4������FH=��
t2+t+4������FH=�� ![]() t2+t+4��FG=t���ȸ��������ε������ʽ���S��OBF=
t2+t+4��FG=t���ȸ��������ε������ʽ���S��OBF= ![]() OBFH=��t2+2t+8��S��OFC=
OBFH=��t2+2t+8��S��OFC= ![]() OCFG=2t������S�ı���ABFC=S��AOC+S��OBF+S��OFC �� �õ�S�ı���ABFC=��t2+4t+12���t2+4t+12=17����t2��4t+5=0���ɡ�=����4��2��4��5=��4��0���ó�����t2��4t+5=0�⣬�����������������ĵ�F����3�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��x+4�������������y=��
OCFG=2t������S�ı���ABFC=S��AOC+S��OBF+S��OFC �� �õ�S�ı���ABFC=��t2+4t+12���t2+4t+12=17����t2��4t+5=0���ɡ�=����4��2��4��5=��4��0���ó�����t2��4t+5=0�⣬�����������������ĵ�F����3�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��x+4�������������y=�� ![]() x2+x+4�Ķ���D��1��
x2+x+4�Ķ���D��1�� ![]() �����ɵ�E��ֱ��BC�ϣ��õ���E��1��3��������DE=
�����ɵ�E��ֱ��BC�ϣ��õ���E��1��3��������DE= ![]() ��3=
��3= ![]() ������D��E��P��QΪ������ı�����ƽ���ı��Σ���ΪDE��PQ��ֻ��DE=PQ�����P�������ǣ�m����m+4�������Q�������ǣ�m����
������D��E��P��QΪ������ı�����ƽ���ı��Σ���ΪDE��PQ��ֻ��DE=PQ�����P�������ǣ�m����m+4�������Q�������ǣ�m���� ![]() m2+m+4��������������������ۣ��ٵ�0��m��4ʱ��PQ=����
m2+m+4��������������������ۣ��ٵ�0��m��4ʱ��PQ=���� ![]() m2+m+4��������m+4��=��
m2+m+4��������m+4��=�� ![]() m2+2m���ⷽ�̩�
m2+2m���ⷽ�̩� ![]() m2+2m=
m2+2m= ![]() �����m��ֵ���õ�P1��3��1�����ڵ�m��0��m��4ʱ��PQ=����m+4��������
�����m��ֵ���õ�P1��3��1�����ڵ�m��0��m��4ʱ��PQ=����m+4�������� ![]() m2+m+4��=
m2+m+4��= ![]() m2��2m���ⷽ��
m2��2m���ⷽ�� ![]() m2��2m=
m2��2m= ![]() �����m��ֵ���õ�P2��2+
�����m��ֵ���õ�P2��2+ ![]() ��2��
��2�� ![]() ����P3��2��
����P3��2�� ![]() ��2+
��2+ ![]() ��������������1���ԣ���2������ˮƽ����Ǧ���߳˻���һ�룬�������BCF��������������������F���꣬��Ϊ�������⣮��3����ΪPQ��DE������ֻ��PQ=AC���ɣ����PQ�IJ������ȱ����ʽ��⣮
��������������1���ԣ���2������ˮƽ����Ǧ���߳˻���һ�룬�������BCF��������������������F���꣬��Ϊ�������⣮��3����ΪPQ��DE������ֻ��PQ=AC���ɣ����PQ�IJ������ȱ����ʽ��⣮
�����㾫�����������⣬������Ҫ�˽�ȷ��һ�κ����ı���ʽ(ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����)����Ҫ����ƽ���ı��ε��ж�(����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı���)�����֪ʶ���Ǵ���Ĺؼ���


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C�ǻ�AD���е㣬��CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�DAC=��ABC����AD=CB���۵�P�ǡ�ACQ�����ģ���AC2=AEAB����CB��GD��������ȷ�Ľ����ǣ� �� 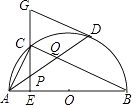
A.�٢ۢ�
B.�ڢܢ�
C.�٢ڢ�
D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
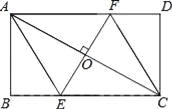
����Ŀ����ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ���AC���е�O��EF��AC����BC�ڵ�E����AD�ڵ�F������AE��CF��
��1����֤���ı���AECF�����Σ�
��2����AB=![]() ����DCF=30�������ı���AECF�������������������ţ�
����DCF=30�������ı���AECF�������������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��AB��һ�㣬BE=2��AE=3��P��AC��һ���㣬��PB+PE����Сֵ�ǣ� ����

A. 5 B. 5![]() C. 6 D.
C. 6 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
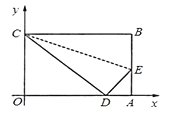
����Ŀ����ͼ���ı���OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ����A��x���ϣ���C��y���ϣ�A������Ϊ��10, 0����C������Ϊ��0, 6��������BC�۵���ʹ��B���ڱ�OA�ϵĵ�D�������߶�EA �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ���A��3��2����B��1��3������AOB�Ƶ�O��ʱ����ת90���õ���A1OB1 �� 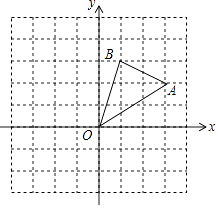
��1����A���ڵ�O���ĶԳƵĵ�P������Ϊ��
��2���������ڻ�����A1OB1��
��3����A1��B1������ֱ�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD���ڵ�O��MΪAD�е㣬����CM��BD�ڵ�N����ON=1�� 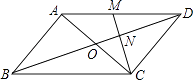
��1����BD�ij���
��2������DCN�����Ϊ2�����ı���ABNM�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ,
��1��2x2y��[3xy2+2��xy2+2x2y��]������x=![]() ��y=��2��
��y=��2��
��2����֪a+b=4��ab=��2�������ʽ��4a��3b��2ab������a��6b��ab����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com