
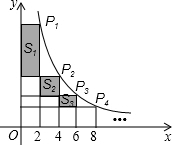
 如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)
如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示) 分析 过点P1、点Pn作y轴的垂线段,垂足分别是点A、B,过点P1作x轴的垂线段,垂足是点C,P1C交BPn于点D,所有的阴影部分平移到左边,阴影部分的面积之和就等于矩形P1ABD的面积,即可得到答案.
解答 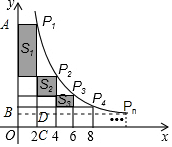 解:如图,过点P1、点Pn作y轴的垂线段,垂足分别是点A、B,过点P1作x轴的垂线段,垂足是点C,P1C交BPn于点D,
解:如图,过点P1、点Pn作y轴的垂线段,垂足分别是点A、B,过点P1作x轴的垂线段,垂足是点C,P1C交BPn于点D,
则点Pn的坐标为(2n,$\frac{5}{n}$),
则OB=$\frac{5}{n}$,
∵点P1的横坐标为2,
∴点P1的纵坐标为5,
∴AB=5-$\frac{5}{n}$,
∴S1+S2+S3+…+Sn=S矩形AP1DB=2(5-$\frac{5}{n}$)=10-$\frac{10}{n+1}$,
故答案为:10-$\frac{10}{n+1}$.
点评 本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,也考查了图形的平移以及矩形的性质,难度适中.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
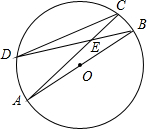 如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.
如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48 | B. | 60 | C. | 96 | D. | 160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com