
 如图,已知在直角坐标系中,直角梯形OABC的直角腰在y轴上,底边OC在x轴上,且∠BCO=45°,点B的坐标是(3,4).
如图,已知在直角坐标系中,直角梯形OABC的直角腰在y轴上,底边OC在x轴上,且∠BCO=45°,点B的坐标是(3,4).分析 (1)如图1中,作BM⊥OC于M.求出OA、OC的长即可解决问题.
(2)①如图2中,设经过t秒,⊙P与BC所在的直线相切于点F,连结PF,由勾股定理可求出PB=$\sqrt{2}$,根据t=OA+AB-PB=(7-$\sqrt{2}$)秒,即可解决问题.
②如图3中,当P在OA上运动时,0≤t<4.根据S△BPD=S梯形OABC-S△APB-S△DPO-S△BCD=8,(或S△BPD=S梯形OABD-S△APB-S△DPO=8),列出方程即可解决问题.
解答 解:(1)如图1中,作BM⊥OC于M.
∵B(3,4),∠BCO=45°,∠BMD=90°,
∴OM=3,BM=4,∠MBD=∠MCB=45°,
∴MC=BM=4,OC=7,
A(0,4)、,C(7,0),
故答案为(0,4),(7,0).
(2)①如图2中,
设经过t秒,⊙P与BC所在的直线相切于点F,连结PF,
∴∠PFB=90°,
∵AB∥OC,∠BCO=45°,
∴∠FBP=45°,
即:PF=FB=1,
由勾股定理可得:PB=$\sqrt{2}$,
∴t=OA+AB-PB=(7-$\sqrt{2}$)秒,
∴当t为(7-$\sqrt{2}$)秒时,⊙P与BC所在的直线相切.
②如图3中,当P在OA上运动时,0≤t<4.
由S△BPD=S梯形OABC-S△APB-S△DPO-S△BCD=8,
(或S△BPD=S梯形OABD-S△APB-S△DPO=8)得
$\frac{1}{2}$ (3+7)×4-$\frac{1}{2}$×3×(4-t)-$\frac{1}{2}$t(7-t)-$\frac{1}{2}$t×4=8,
整理,得t2-8t+12=0,解之得t1=2,t2=6(舍),
当P在AB上运动,4≤t<7.
由S△BPD=$\frac{1}{2}$×(7-t)×4=8,得t=3(舍),
∴当t=2时,以B、P、R为顶点的三角形的面积为8.
点评 本题考查圆综合题、矩形的判定和性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识,学会利用分割法求三角形的面积,学会把问题转化为方程解决,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
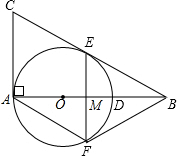 如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E.
如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
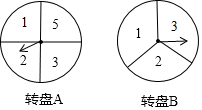 分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图所示),小明、小强两人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则小明胜;若指针所指两区域的数字之积为偶数,则小强胜;若有指针落在分割线上,则无效,需重新转动转盘.
分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图所示),小明、小强两人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则小明胜;若指针所指两区域的数字之积为偶数,则小强胜;若有指针落在分割线上,则无效,需重新转动转盘.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
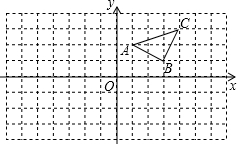 已知:如图所示.
已知:如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com