
【题目】阅读下面材料,完成相应任务:



(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() , , ,则四边形
, , ,则四边形![]() ≌四边形
≌四边形![]() ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题.
【答案】(1)假;(2)见解析;(3) ![]() ,
,![]() .
.
【解析】
(1)连接AC,延长BC到E,过点E作EF∥CD,交AD的延长线于点F,则∠E=∠BCD,∠F=∠ADC,将四边形ABEF平移得到四边形A′B′C′D′,则AB=A′B′,∠A=∠A′,∠B=∠B′,∠C=∠C′,∠D=∠D′,而BC≠B′C′,AD≠A′D′,得出四边形ABCD和四边形A′B′C′D′不全等,即可得出结论;
(2)连接BD,B′D′,证明△ABD≌△A′B′D′,得出BD=B′D′,∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,再证明△BCD≌△B′C′D′,得出∠C=∠C′,∠CBD=∠C′B′D′,∠BDC=∠B′D′C′,证出∠ABC=∠A′B′C′,∠CDA=∠C′D′A′,即可得出结论;
(3)连接AC、A′C′,证明△ABC≌△A′B′C′,得出AC=A′C′,∠BAC=∠B′A′C′,∠BCA=∠B′C′A′,得出∠ACD=∠A′C′D′,再证明△ACD≌△A′C′D′,得出AD=A′D′,∠D=∠D′,∠CAD=∠C′A′D′,证出∠BAD=∠B′A′D′,即可得出结论.
(1)假;
(2)连接BD、B’D’

在△ABD与 △A’B’D’中
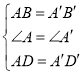
∴△ABD≌△A’B’D’(SAS)
∴BD=B’D’ ∠ABD=∠A’B’D’ ∠ADB=∠A’D’B’
在△BCD与 △B’C’D’中
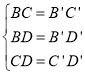
∴△BCD≌△B’C’D’(SSS)
∴∠C=∠C’ ∠CBD=∠C’B’D’ ∠CDB=∠C’D’B’
∴∠ABD+∠CBD=∠A’B’D’+∠C’B’D’
∠ADB+∠CDB=∠A’D’B’+∠C’D’B’
即∠ABC=∠A’B’C’ ∠ADC=∠A’D’C’
∴四边形![]() ≌四边形
≌四边形![]()
(3)![]() ,∠C=∠C’
,∠C=∠C’


科目:初中数学 来源: 题型:
【题目】在等边三角形ABC,点D在BC上,点E在AG的延长线上,DE=DA(如图1).

(1)求证:∠BAD=∠EDC;
(2)如图2,若点E关于直线BC的对称点为M,连DM,AM,请判断△ADM的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,△ABD为等边三角形,连接CD

(1)求∠ACD的度数
(2)作∠BAC的角平分线交CD于点E,求证:DE=AE+CE
(3)在(2)的条件下,P为图形外一点,满足∠CPB=60°,求证:EP平分∠CPB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 是两个大小不同的等腰直角三角形.
是两个大小不同的等腰直角三角形.
![]() 如图①所示,连接
如图①所示,连接![]() ,
,![]() ,试判断线段
,试判断线段![]() 和
和![]() 的数量和位置关系,并说明理由;
的数量和位置关系,并说明理由;
![]() 如图②所示,连接
如图②所示,连接![]() ,将线段
,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,试判断线段
,试判断线段![]() 和
和![]() 的数量和位置关系,并说明理由.
的数量和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△![]() ,按以下步骤作图:①分别以
,按以下步骤作图:①分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]()
![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() 、
、![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则下列结论中不一定成立的是( )
,则下列结论中不一定成立的是( )
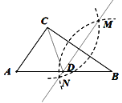
A.![]() B.△
B.△![]() 是等边三角形
是等边三角形
C.点D是AB的中点D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;若正八边形作环状连接,中间可以围的正多边形的边数为;

若正八边形作环状连接,中间可以围的正多边形的边数为________,若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
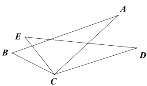
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场服装柜在销售中发现:某童装平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,调查发现:如果每件童装降价
元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,调查发现:如果每件童装降价![]() 元,那么平均每天就可多售出
元,那么平均每天就可多售出![]() 件.要想平均每天销售这种童装共盈利
件.要想平均每天销售这种童装共盈利![]() 元,设每件童装降价
元,设每件童装降价![]() 元,那么应满足的方程是________.
元,那么应满足的方程是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com