
����Ŀ����ͼ��ֱ��y����x+5��x�ύ�ڵ�B����y�ύ�ڵ�D��������y����x2+bx+c��ֱ��y����x+5����B��D���㣬��C�������ߵĶ��㣮

��1���������ߵĽ���ʽ��
��2����M��ֱ��BD�Ϸ��������ϵ�һ�����㣬�������Ϊm������M��x��Ĵ��ߣ���ֱ��BD�ڵ�P�����߶�PM�ij������ʱ����m��ֵ��PM�����ֵ��
��3�������������Ƿ��������B��D�ĵ�Q��ʹ��BDQ��BD���ϵĸ�Ϊ3![]() �������������Q�����ꣻ����������˵�����ɣ�
�������������Q�����ꣻ����������˵�����ɣ�
���𰸡���1�������ߵı���ʽΪ��y����x2+4x+5����2����m��![]() ʱ��PM�����ֵ
ʱ��PM�����ֵ![]() ����3���������������ĵ�Q��������ΪQ1��2��9����Q2��3��8����Q3����1��0����Q4��6����7����
����3���������������ĵ�Q��������ΪQ1��2��9����Q2��3��8����Q3����1��0����Q4��6����7����
��������
��1��y=-x+5����x=0����y=5����y=0����x=5���ʵ�B��D������ֱ�Ϊ��5��0������0��5�������ô���ϵ����������⣻
��2��������ɵ�M������Ϊ��m����m2+4m+5��������P������Ϊ��m����m+5������ʾ��PM�ij��ȣ�PM=-m2+4m+5-��-m+5��=-m2+5m=-��m-![]() ��2+
��2+![]() �����ö��κ��������ʼ�����⣻
�����ö��κ��������ʼ�����⣻
��3����Q��QG��y�ύBD�ڵ�G����x���ڵ�E����QH��BD��H�����Q������Q��x����x2+4x+5������G��x����x+5������ʾ��QG�ij���QG=|-x2+4x+5-��-x+5��|=|-x2+5x|���������ɵá�BOD�ǵ���ֱ�������Σ�����֤�á�QHGΪ����ֱ�������Σ���BDQ��BD���ϵĸ�Ϊ3![]() ʱ����QH=HG=3
ʱ����QH=HG=3![]() ��QG=
��QG=![]() ��3
��3![]() =6��|-x2+5x|=6��������⣮
=6��|-x2+5x|=6��������⣮
�⣺��1��y����x+5����x��0����y��5����y��0����x��5��
�ʵ�B��D������ֱ�Ϊ��5��0������0��5����
����κ�������ʽΪ��y����x2+bx+5������B���������ʽ����ã�b��4��
�������ߵı���ʽΪ��y����x2+4x+5��
��2����M�������Ϊm��m��0������P��m����m+5����M��m����m2+4m+5����
��PM����m2+4m+5������m+5������m2+5m������m-![]() ��2+
��2+![]() ��
��
�൱m��![]() ʱ��PM�����ֵ
ʱ��PM�����ֵ![]() ��
��
��3����ͼ����Q��QG��y�ύBD�ڵ�G����x���ڵ�E����QH��BD��H��
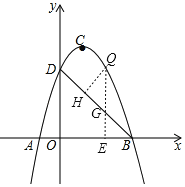
��Q��x����x2+4x+5������G��x����x+5����
��QG��|��x2+4x+5������x+5��|��|��x2+5x|��
�ߡ�BOD�ǵ���ֱ�������Σ�
���DBO��45����
���HGQ����BGE��45����
���QHG�ǵ���ֱ�������Σ�
����BDQ��BD���ϵĸ�Ϊ3![]() ʱ����QH��HG��3
ʱ����QH��HG��3![]() ��
��
��QG��![]() ��3
��3![]() ��6��
��6��
��|��x2+5x|��6��
����x2+5x��6ʱ�����x��2��x��3��
��Q��2��9����3��8����
����x2+5x����6ʱ�����x����1��x��6��
��Q����1��0����6����7����
���Ͽ�֪�������������ĵ�Q��������ΪQ1��2��9����Q2��3��8����Q3����1��0����Q4��6����7����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ��ֱ�߹���(0��4)������������y��![]() x2����A��B���㣬���е�A�ĺ������ǣ�2.
x2����A��B���㣬���е�A�ĺ������ǣ�2.
(1)������ֱ�ߵĽ���ʽ����B�����ꣻ
(2)��x�����Ƿ���ڵ�C��ʹ�á�ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
(3)���߶�AB��һ��P����PM��x�ᣬ���������ڵ�M����M�ڵ�һ���ޣ���N(0��1)������M�ĺ�����Ϊ��ֵʱ��MN��3MP�ij���������ֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һö�ʵؾ��ȵ����ӣ������������沢�ֱ��������1��2��3��4��5��6.��ͼ2����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() 7��Ȧ����������Ȧ������.��Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ��������ϵ�һ���ϵ������Ǽ����ʹ�Ȧ
7��Ȧ����������Ȧ������.��Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ��������ϵ�һ���ϵ������Ǽ����ʹ�Ȧ![]() ��ʼ��ǰ�������������.�磺��Ȧ
��ʼ��ǰ�������������.�磺��Ȧ![]() ��������һ������3����������3����࣬����Ȧ
��������һ������3����������3����࣬����Ȧ![]() �����ڶ�������3���ʹ�
�����ڶ�������3���ʹ�![]() ��ʼ������3����࣬����Ȧ
��ʼ������3����࣬����Ȧ![]() �����ڶ�������4���ʹ�Ȧ
�����ڶ�������4���ʹ�Ȧ![]() ��ʼ������4����࣬����Ȧ
��ʼ������4����࣬����Ȧ![]() �ص�Ȧ
�ص�Ȧ![]() ��������Ϸ�ߴ�Ȧ
��������Ϸ�ߴ�Ȧ![]() ����.
����.
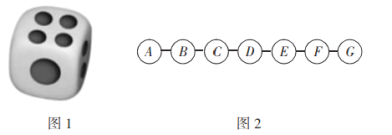
��1��С�������һ�����ӣ�������Ȧ![]() �ĸ���
�ĸ���![]() ��
��
��2��С��������������ӣ����б�������״ͼ�����������Ȧ![]() �ĸ���
�ĸ���![]() ����ָ������С������Ȧ
����ָ������С������Ȧ![]() �Ŀ�����һ����
�Ŀ�����һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2 +bx+ 4��x�����������ֱ�ΪA����4��0����B��2��0������y�ύ�ڵ�C������ΪD��E��1��2��Ϊ�߶�BC���е㣬BC�Ĵ�ֱƽ������x�ᡢy��ֱ���F��G��
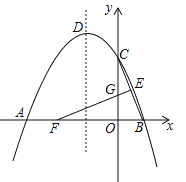
��1���������ߵĺ�������ʽ����д������D�����ꣻ
��2����ֱ��EF����һ��H��ʹ��CDH���ܳ���С���������С�ܳ���
��3������K��x���Ϸ������������˶�����K�˶���ʲôλ��ʱ��
��EFK�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
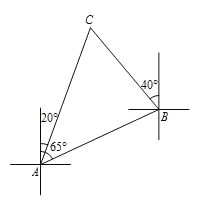
����Ŀ����ͼ��һ�Ҵ���A���ر�ƫ��65��������![]() km��B�ۣ�Ȼ�����ر�ƫ��40����������C�ۣ�C����A�۱�ƫ��20������.
km��B�ۣ�Ȼ�����ر�ƫ��40����������C�ۣ�C����A�۱�ƫ��20������.
��1����C�Ķ�����
��2��A��C����֮��ľ���Ϊ����km.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��ӯ��40Ԫ.Ϊ�������ۣ�����ӯ�����̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2��.
��1��ÿ���������۶���Ԫʱ���̳�ƽ��ÿ���ӯ����1050Ԫ��
��2��ÿ���������۶���Ԫʱ���̳�ƽ��ÿ��ӯ��������ӯ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���![]() ��a��bΪ��������
��a��bΪ��������![]() ���뷴��������
���뷴��������![]() ��mΪ��������
��mΪ��������![]() ����ͼ���ڵ�A����2��1����B��1��n����
����ͼ���ڵ�A����2��1����B��1��n����

��1������������һ�κ����Ľ���ʽ��
��2������OA��OB������AOB�������
��3��ֱ��д����![]() ʱ���Ա���x��ȡֵ��Χ��
ʱ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������ͼ1��AB����O���ң���F��![]() ���е㣬����F��EF��AB�ڵ�E���õ�E��AB���е㣬��AE��EB����O��һ��C��AC��BC����������ACB��Ϊ��O��һ�������ҡ���
���е㣬����F��EF��AB�ڵ�E���õ�E��AB���е㣬��AE��EB����O��һ��C��AC��BC����������ACB��Ϊ��O��һ�������ҡ���
��1������C����AB���Ϸ�ʱ����ͼ2��������F��EF��AC�ڵ�E����֤����E�ǡ�����ACB�����е㣬��AE��EC+CB��
��2������C����AB���·�ʱ����ͼ3���������������䣬�����������Ƿ���Ȼ������������˵�����ɣ�������������ôAE��EC��CB����������������ϵ��ֱ��д��������֤����
��3����ͼ4����֪Rt��ABC�У���C��90�㣬��BAC��30�㣬Rt��ABC�����Բ��O�İ뾶Ϊ2������O��һ��P��PH��AC�ڵ�H����AB�ڵ�M������PAB��45��ʱ����AH�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
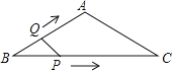
����Ŀ����ͼ���ڵ�����ABC�У�AB=AC=4cm����B=30������P�ӵ�B��������![]() cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B������2cm/s���ٶ���B��A��C�˶�����Cֹͣ������BPQ�����Ϊy�˶�ʱ��Ϊx��s����������ͼ�����ܴ��·�ӳy��x֮���ϵ���ǣ�������
cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B������2cm/s���ٶ���B��A��C�˶�����Cֹͣ������BPQ�����Ϊy�˶�ʱ��Ϊx��s����������ͼ�����ܴ��·�ӳy��x֮���ϵ���ǣ�������
A.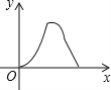 B.
B.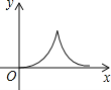 C.
C.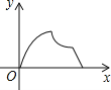 D.
D.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com