
”¾ĢāÄæ”æ”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬AC£½BC£¬”ĻACB£½90”ć
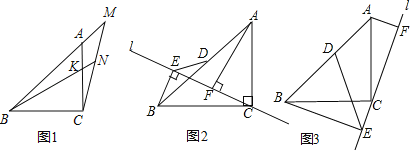
£Ø1£©ČēĶ¼1£¬µćMŹĒBAŃÓ³¤ĻßÉĻŅ»µć£¬Į¬½įCM£¬KŹĒACÉĻŅ»µć£¬BKŃÓ³¤Ļß½»CMÓŚN£¬”ĻMBN£½”ĻMCA£½15”ć£¬BK£½8£¬ĒóCMµÄ³¤¶Č£»
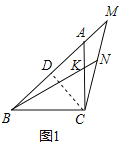
£Ø2£©ČēĶ¼2£¬Ö±Ļßl¾¹żµćC£¬AF”ĶlÓŚµćF£¬BE”ĶlÓŚµćE£¬µćDŹĒABµÄÖŠµć£¬Į¬½ÓED£¬ĒóÖ¤£ŗAF£½BE+![]() DE£»
DE£»
£Ø3£©½«Ķ¼2ÖŠµÄÖ±ĻßlŠż×Ŗµ½”÷ABCµÄĶā²æ£¬ĘäĖūĢõ¼ž²»±ä£¬ĒėĒó³öAF”¢BE”¢DEµÄ¹ŲĻµ£®²¢Š“³ö±ŲŅŖµÄ²½Öč£®
”¾“š°ø”æ£Ø1£©4![]() £»£Ø2£©AF=BE+
£»£Ø2£©AF=BE+![]() DE£¬¼ū½āĪö£»£Ø3£©AF+BE£½
DE£¬¼ū½āĪö£»£Ø3£©AF+BE£½![]() DE£¬¼ū½āĪö
DE£¬¼ū½āĪö
”¾½āĪö”æ
£Ø1£©¹żC×÷CD”ĶABÓŚD£¬ÓɵČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæɵƔĻABC£½”ĻBAC£½45”ć£¬½ų¶ųČ·¶Ø”ĻKBC£½30”ć£¬øł¾ŻÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½BC£½4![]() £¬ĒóµĆCD£½
£¬ĒóµĆCD£½![]() BC£½2
BC£½2![]() £¬½āÖ±½ĒČż½ĒŠĪ¼“æɵƵ½½įĀŪ£»
£¬½āÖ±½ĒČż½ĒŠĪ¼“æɵƵ½½įĀŪ£»
£Ø2£©ČēĶ¼2£¬Į¬½ÓDF£¬CD£¬øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½CD£½BD£¬”ĻCDB£½90”ć£¬ÓÉČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½BE£½CF£¬CE£½AF£¬ĶĘ³ö”÷BDE”Õ”÷CDF£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻEDB£½”ĻFDC£¬DE£½DF£¬øł¾ŻÓą½ĒµÄŠŌÖŹµĆµ½”ĻEDF£½90”ć£¬øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½EF£½![]() DE£¬ÓŚŹĒµĆµ½½įĀŪ£»
DE£¬ÓŚŹĒµĆµ½½įĀŪ£»
£Ø3£©½įĀŪ£ŗBE+AF£½![]() DE£¬Į¬½ÓCD£¬DF£¬ÓÉ£Ø2£©Ö¤µĆ”÷BCE”Õ”÷ACF£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½BE£½CF£¬CE£½AF£¬ÓÉ£Ø2£©Ö¤µĆ”÷DEFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½EF£½
DE£¬Į¬½ÓCD£¬DF£¬ÓÉ£Ø2£©Ö¤µĆ”÷BCE”Õ”÷ACF£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½BE£½CF£¬CE£½AF£¬ÓÉ£Ø2£©Ö¤µĆ”÷DEFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½EF£½![]() DE£¬¼“æɵƵ½½įĀŪ£®
DE£¬¼“æɵƵ½½įĀŪ£®
½ā£ŗ£Ø1£©¹żC×÷CD”ĶABÓŚD£¬
”ßAC£½BC£¬”ĻACB£½90”ć£¬
”ą”ĻABC£½”ĻBAC£½45”ć£¬
”ß”ĻMBN£½15”ć£¬
”ą”ĻKBC£½30”ć£¬
”ßBK£½8£¬
”ąBC£½4![]() £¬
£¬
”ąCD£½![]() BC£½2
BC£½2![]()
”ß”ĻMCA£½15”ć£¬”ĻBAC£½45”ć£¬
”ą”ĻM£½30”ć£¬
”ąCM£½2CD£½4![]() £»
£»
£Ø2£©”ßBE”ĶCE£¬
”ą”ĻBEC£½”ĻACB£½90”ć£¬
”ą”ĻEBC+”ĻBCE£½”ĻBCE+”ĻACF£½90”ć£¬
”ą”ĻEBC£½”ĻACF£¬
”ßAF”ĶlÓŚµćF£¬
”ą”ĻAFC£½90”ć£¬
ŌŚ”÷BCEÓė”÷ACFÖŠ£¬
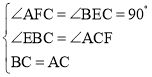 £¬
£¬
”ą”÷ACF”Õ”÷CBE£ØAAS£©£¬
ČēĶ¼2£¬Į¬½ÓDF£¬CD£¬
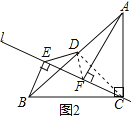
”ßµćDŹĒABµÄÖŠµć£¬
”ąCD£½BD£¬”ĻCDB£½90”ć£¬
”ß”÷ACF”Õ”÷CBE£¬
”ąBE£½CF£¬CE£½AF£¬
”ß”ĻEBD£½”ĻDCF£¬
ŌŚ”÷BDEÓė”÷CDFÖŠ£¬
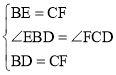 £¬
£¬
”ą”÷BDE”Õ”÷CDF£ØSAS£©£¬
”ą”ĻEDB£½”ĻFDC£¬DE£½DF£¬
”ß”ĻCDF+”ĻFDB£½90”ć£¬”ĻEDB+”ĻBDF£½90”ć£¬
”ą”ĻEDF£½90”ć£¬
”ą”÷EDFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąEF£½![]() DE£¬
DE£¬
”ąAF£½CE£½EF+CF£½BE+![]() DE£»
DE£»
£Ø3£©ČēĶ¼3£¬Į¬½ÓCD£¬DF£¬
ÓÉ£Ø2£©Ö¤µĆ”÷BCE”Õ”÷ACF£¬
”ąBE£½CF£¬CE£½AF£¬
ÓÉ£Ø2£©Ö¤µĆ”÷DEFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąEF£½![]() DE£¬
DE£¬
”ßEF£½CE+CF£½AF+BE£½![]() DE£®
DE£®
¼“AF+BE£½![]() DE£®
DE£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōÕż±ČĄżŗÆŹży=kx(k”Ł0)µÄĶ¼Ļó¾¹żµćP(2,3),ŌņøĆŗÆŹżµÄĶ¼Ļó¾¹żµÄµćŹĒ( )
A.(3,2)B.(1,6)C.(2,3)D.(1,6)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB£½3£¬BC£½5£¬µćEŌŚAD±ßÉĻĒŅ²»ÓėµćAŗĶµćDÖŲŗĻ£¬µćOŹĒ¶Ō½ĒĻßBDµÄÖŠµć£¬µ±”÷OEDŹĒµČŃüČż½ĒŠĪŹ±£¬AEµÄ³¤ĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
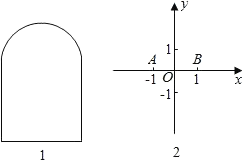
”¾ĢāÄæ”æŅŃÖŖĘ½ĆęĶ¼ŠĪS£¬µćP”¢QŹĒSÉĻČĪŅāĮ½µć£¬ĪŅĆĒ°ŃĻ߶ĪPQµÄ³¤¶ČµÄ×ī“óÖµ³ĘĪŖĘ½ĆęĶ¼ŠĪSµÄ”°æķ¾ą”±£®ĄżČē£¬Õż·½ŠĪµÄæķ¾ąµČÓŚĖüµÄ¶Ō½ĒĻߵij¤¶Č£®
£Ø1£©Š“³öĻĀĮŠĶ¼ŠĪµÄæķ¾ą£ŗ
¢Ł°ė¾¶ĪŖ1µÄŌ²£ŗ”” ””£»
¢ŚČēĶ¼1£¬ÉĻ·½ŹĒ°ė¾¶ĪŖ1µÄ°ėŌ²£¬ĻĀ·½ŹĒÕż·½ŠĪµÄČżĢõ±ßµÄ”°“°»§ŠĪ”°£ŗ”” ””£»
£Ø2£©ČēĶ¼2£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖµćA£Ø©1£¬0£©”¢B£Ø1£¬0£©£¬CŹĒ×ų±źĘ½ĆęÄŚµÄµć£¬Į¬½ÓAB”¢BC”¢CAĖłŠĪ³ÉµÄĶ¼ŠĪĪŖS£¬¼ĒSµÄæķ¾ąĪŖd£®
¢ŁČōd£½2£¬ĒóµćCĖłŌŚµÄĒųÓņµÄĆ껿£»
¢ŚČōµćCŌŚ”ŃMÉĻŌĖ¶Æ£¬”ŃMµÄ°ė¾¶ĪŖ1£¬Ō²ŠÄMŌŚ¹żµć£Ø0£¬2£©ĒŅÓėyÖį“¹Ö±µÄÖ±ĻßÉĻ£®¶ŌÓŚ”ŃMÉĻČĪŅāµćC£¬¶¼ÓŠ5”Üd”Ü8£¬Ö±½ÓŠ“³öŌ²ŠÄMµÄŗį×ų±źxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻÓėŹµ¼ł£ŗ¾ŲŠĪµÄŠż×Ŗ
ĪŹĢāĒé¾³£ŗ
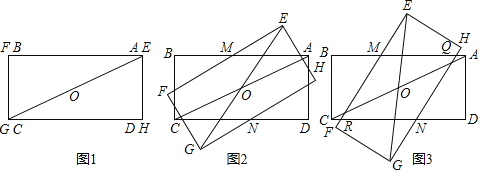
ŌŚ×ŪŗĻÓėŹµ¼łæĪÉĻ£¬ĄĻŹ¦ČĆĶ¬Ń§ĆĒŅŌ”°¾ŲŠĪµÄŠż×Ŗ”±ĪŖÖ÷ĢāæŖÕ¹ŹżŃ§»ī¶Æ£®¾ßĢåŅŖĒó£ŗČēĶ¼1£¬½«³¤Óėæķ¶¼ĻąµČµÄĮ½øö¾ŲŠĪÖ½Ę¬ABCDŗĶEFGHµž·ÅŌŚŅ»Ęš£¬ÕāŹ±¶Ō½ĒĻßACŗĶEG»„ĻąÖŲŗĻ£®¹Ģ¶Ø¾ŲŠĪABCD£¬½«¾ŲŠĪEFGHČĘACµÄÖŠµćOÄꏱÕė·½ĻņŠż×Ŗ£¬Ö±µ½µćEÓėµćBÖŲŗĻŹ±Ķ£Ö¹£¬ŌŚ“Ė¹ż³ĢÖŠæŖÕ¹Ģ½¾æ»ī¶Æ£®
²Ł×÷·¢ĻÖ£ŗ
£Ø1£©ŠŪÓ„Š”×é³õ²½·¢ĻÖ£ŗŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±±ßABÓėEF½»ÓŚµćM£¬±ßCDÓėGH½»ÓŚµćN£¬ČēĶ¼2”¢Ķ¼3ĖłŹ¾£¬ŌņĻ߶ĪAMÓėCNŹ¼ÖÕ“ęŌŚµÄŹżĮæ¹ŲĻµŹĒ”” ””£®
£Ø2£©ŠŪÓ„Š”×é¼ĢŠųĢ½¾æ·¢ĻÖ£ŗŌŚŠż×ŖæŖŹ¼ŗ󣬵±Į½øö¾ŲŠĪÖ½Ę¬ÖŲµž²æ·ÖĪŖĖıߊĪQMRNŹ±£¬ČēĶ¼3ĖłŹ¾£¬ĖıߊĪQMRNĪŖĮāŠĪ£¬ĒėÄćÖ¤Ć÷Õāøö½įĀŪ£®
£Ø3£©ŠŪÓ„Š”×黹·¢ĻÖŌŚĪŹĢā£Ø2£©ÖŠµÄĖıߊĪQMRNÖŠ”ĻMQNÓėŠż×Ŗ½Ē”ĻAOE“ęŌŚ×ÅĢŲ¶ØµÄŹżĮæ¹ŲĻµ£¬ĒėÄ抓³öÕāŅ»¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
Źµ¼łĢ½¾æ£ŗ
£Ø4£©ŌŚĶ¼3ÖŠ£¬ĖęמŲŠĪÖ½Ę¬EFGHµÄŠż×Ŗ£¬ĖıߊĪQMRNµÄĆ껿»į·¢Éś±ä»Æ£®Čō¾ŲŠĪÖ½Ę¬µÄ³¤ĪŖ![]() £¬æķĪŖ
£¬æķĪŖ![]() £¬ĒėÄć°ļÖśŠŪÓ„Š”×éĢ½¾æµ±Šż×Ŗ½Ē”ĻAOEĪŖ¶ąÉŁ¶ČŹ±£¬ĖıߊĪQMRNµÄĆ껿×ī“ó£æ×ī“óĆ껿ŹĒ¶ąÉŁ£æ£ØÖ±½ÓŠ“³ö“š°ø£©
£¬ĒėÄć°ļÖśŠŪÓ„Š”×éĢ½¾æµ±Šż×Ŗ½Ē”ĻAOEĪŖ¶ąÉŁ¶ČŹ±£¬ĖıߊĪQMRNµÄĆ껿×ī“ó£æ×ī“óĆ껿ŹĒ¶ąÉŁ£æ£ØÖ±½ÓŠ“³ö“š°ø£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŌ×ų±źŌµćĪŖŌ²ŠÄ£¬1ĪŖ°ė¾¶µÄŌ²·Ö±š½»x£¬yÖįµÄÕż°ėÖįÓŚµćA£¬B£®
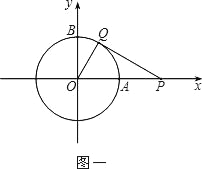
£Ø1£©ČēĶ¼Ņ»£¬¶ÆµćP“ÓµćA“¦³ö·¢£¬ŃŲxÖįĻņÓŅŌČĖŁŌĖ¶Æ£¬Óė“ĖĶ¬Ź±£¬¶ÆµćQ“ÓµćB“¦³ö·¢£¬ŃŲŌ²ÖÜ°“Ė³Ź±Õė·½ĻņŌČĖŁŌĖ¶Æ£®ČōµćQµÄŌĖ¶ÆĖŁ¶Č±ČµćPµÄŌĖ¶ÆĖŁ¶ČĀż£¬¾¹ż1ĆėŗóµćPŌĖ¶Æµ½µć£Ø2£¬0£©£¬“ĖŹ±PQĒ”ŗĆŹĒ”ŃOµÄĒŠĻߣ¬Į¬½ÓOQ£®Ēó”ĻQOPµÄ“󊔣»
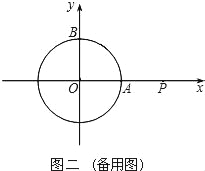
£Ø2£©ČōµćQ°“ÕÕ£Ø1£©ÖŠµÄ·½ĻņŗĶĖŁ¶Č¼ĢŠųŌĖ¶Æ£¬µćPĶ£ĮōŌŚµć£Ø2£¬0£©“¦²»¶Æ£¬ĒóµćQŌŁ¾¹ż5ĆėŗóÖ±ĻßPQ±»”ŃO½ŲµĆµÄĻŅ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ė®Ę½µŲĆęÉĻÓŠŅ»“±øßĪŖADµÄĀ„£¬Ā„Ē°ÓŠĘĀ½ĒĪŖ30”ć”¢³¤ĪŖ6Ć׵Ċ±ĘĀ£®ŅŃÖŖ“ÓAµć¹Ū²āB”¢CµÄø©½Ē·Ö±šĪŖ60”ćŗĶ30”ć
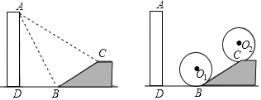
£Ø1£©ĒóĀ„øߣ»
£Ø2£©ĻÖŌŚŅŖ½«Ņ»øö°ė¾¶ĪŖ2Ć׵ĔŃO“ÓĘĀµ×ÓėŠ±ĘĀĻąĒŠŹ±µÄ”ŃO1Ī»ÖĆĒ£Ņż¹ö¶Æµ½Š±ĘĀÉĻÖĮŌ²øÕŗĆÓėŠ±ĘĀÉĻĖ®Ę½ĆęĻąĒŠŹ±µÄ”ŃO2Ī»ÖĆ£¬Ēó¹ö¶Æ¹ż³ĢÖŠŌ²ŠÄOŅĘ¶ÆµÄ×ܳ¤¶Č£®£Ø²Īæ¼Źż¾Ż£ŗtan15”ć£½2©![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
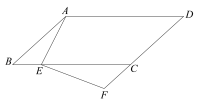
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”õABCDÖŠ£¬µćEŌŚBC±ßÉĻ£¬µćFŌŚDCµÄŃÓ³¤ĻßÉĻ£¬ĒŅ”ĻDAE=”ĻF£®
£Ø1£©ĒóÖ¤£ŗ”÷ABE”×”÷ECF£»
£Ø2£©ČōAB=5£¬AD=8£¬BE=2£¬ĒóFCµÄ³¤”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
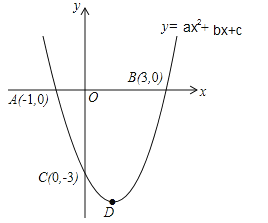
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() µÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø©1.0£©£¬B£Ø3£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬©3£©£¬¶„µćĪŖD£®
µÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø©1.0£©£¬B£Ø3£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬©3£©£¬¶„µćĪŖD£®
£Ø1£©Ēó“ĖÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©Ēó“ĖÅ×ĪļĻ߶„µćDµÄ×ų±źŗĶ¶Ō³ĘÖį£®
£Ø3£©Ģ½¾æ¶Ō³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µćP£¬Ź¹µĆŅŌµćP”¢D”¢AĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³öĖłÓŠ·ūŗĻĢõ¼žµÄPµćµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com