
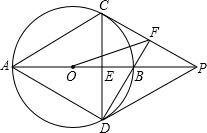
 如图,半径为4的⊙O中直径AB垂直弦CD于E,过C作⊙O的切线CP交AB的延长线于P,连接DB并延长交CP于F,连接AC,AD,PD,OF.
如图,半径为4的⊙O中直径AB垂直弦CD于E,过C作⊙O的切线CP交AB的延长线于P,连接DB并延长交CP于F,连接AC,AD,PD,OF.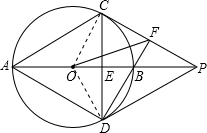 (1)证明:连接OD、OC.
(1)证明:连接OD、OC.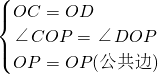 ,
, ,
, ;
; ,∠CDF=30°,则CF=
,∠CDF=30°,则CF= CD=2
CD=2 (30°角所对的直角边是斜边的一半);
(30°角所对的直角边是斜边的一半);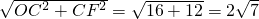 (勾股定理).
(勾股定理).

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为
(2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com