
分析 分两种情况讨论:当AB+AD=30,BC+DC=24或AB+AD=24,BC+DC=30,所以根据等腰三角形的两腰相等和中线的性质可求得,三边长为16,16,22或20,20,14.
解答 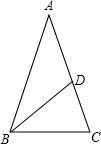 解:设三角形的腰AB=AC=x
解:设三角形的腰AB=AC=x
若AB+AD=24cm,
则:x+$\frac{1}{2}$x=24
∴x=16
三角形的周长为24+30=54(cm)
所以三边长分别为16cm,16cm,22cm;
若AB+AD=30cm,
则:x+$\frac{1}{2}$x=30
∴x=20
∵三角形的周长为24+30=54(cm)
∴三边长分别为20cm,20cm,14cm;
因此,三角形的三边长为16cm,16cm,22cm或20cm,20cm,14cm,
故答案为:16cm,16cm,22cm或20cm,20cm,14cm.
点评 本题主要考查了等腰三角形的性质;解题的关键是利用等腰三角形的两腰相等和中线的性质求出腰长,再利用周长的概念求得边长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为4,将长为4的线段QR的 两 端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,将长为4的线段QR的 两 端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为16-4π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-4 | B. | k<4 | C. | k<4且k≠0 | D. | k>-4 且k≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com