
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线.
(2)若DE+EA=4,⊙O的半径为5,求CF的长度.

【答案】(1)详见解析;(2)CF=18.
【解析】
(1)根据已知条件得到OD∥AC即可,于是得到结论;
(2)如图,过点O作OH⊥AF于点H,构建矩形ODEH,设AH=x.则由矩形的性质推知:AE=5x,OH=DE=4(5x)=x1.在Rt△AOH中,由勾股定理知:x2+(x1)2=52,通过解方程得到AH的长度,结合OH⊥AF,得到AF=2AH=2×4=8,于是得到结论.
(1)∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE⊥AC,OD是半径,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,

∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=4,OD=5,
∴AE=5﹣x,OH=DE=4﹣(5﹣x)=x﹣1.
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣1)2=52,
解得x1=4,x2=﹣3(不合题意,舍去).
∴AH=4.
∵OH⊥AF,
∴AH=FH=![]() AF,
AF,
∴AF=2AH=2×4=8,
∵AC=AB=2OD=10,
∴CF=18.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】画出函数y=2x+1的图象,利用图象求:
(1)方程2x+1=0的根;
(2)不等式2x+1≥0的解集;
(3)当y≤3时,求x的取值范围;
(4)当﹣3≤y≤3时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
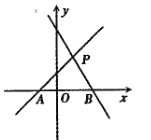
【题目】如图,直线![]() 是一次函数
是一次函数![]() 的图象,直线
的图象,直线![]() 是一次函数
是一次函数![]() 的图象.
的图象.
(1)求A、B、P三点坐标;
(2)求![]() 的面积;
的面积;
(3)已知过P点的直线把![]() 分成面积相等的两部分,求该直线解析式.
分成面积相等的两部分,求该直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
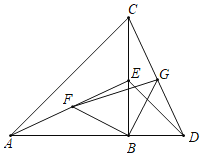
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,E为BC边上一点(不与B、C重合),D为AB延长线上一点且BD=BE.点F、G分别为AE、CD的中点.
(1)求证:AE=CD.
(2)求证:△BFG为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三八宏图展,九州春意浓”,为了解某校1000名学生在2017年3月8日“妇女节”期间对母亲表达祝贺的方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:
某校抽取学生“妇女节”期间对母亲表达祝贺的方式的统计表
方式 | 频数 | 百分比 |
送母亲礼物 | 23 | 46% |
帮母亲做家务 | ||
给母亲一个爱的拥抱 | 8% | |
其他 | 15 | |
合计 | 100% |
(1)本次问卷调查抽取的学生共有 人,其中通过给母亲一个爱的拥抱表达祝贺的学生有 人.
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)根据抽样的结果,估计该校学生通过帮母亲做家务表达祝贺的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
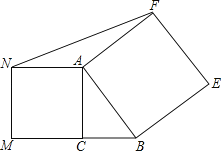
【题目】如图,Rt△ABC,∠ACB=90°.分别以AB,AC为边作正方形ABEF和正方形ACMN,连接FN.若AC=4,BC=3,则S△ANF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则原方程化为y2﹣5y+4=0,解此方程得:y1=1,y2=4.
当y=1时,x2﹣1═1,∴x=±![]() .
.
当y=4时,x2﹣1═4,∴x=±![]() .
.
∴原方程的解为:x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]() .
.
以上方法叫做换元法解方程,达到了降次的目的,体现了转化思想.
运用上述方法解方程:x4﹣8x2+12=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠ACB=90°,AB=AC,点D在直线AB上,连接CD,在CD的右侧作CE⊥CD,CD=CE,

(1)如图1,①点D在AB边上,直接写出线段BE和线段AD的关系;
(2)如图2,点D在B右侧,BD=1,BE=5,求CE的长.
(3)拓展延伸
如图3,∠DCE=∠DBE=90,CD=CE,BC=![]() ,BE=1,请直接写出线段EC的长.
,BE=1,请直接写出线段EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 点向
点向![]() 点运动,设运动时间为
点运动,设运动时间为![]() (秒)
(秒)![]() .
.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度;
的长度;
(2)若点![]() 、
、![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 、
、![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度
的运动速度![]() 为多少时,能够使
为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com