
分析 (1)原式变形后,提取公因式即可得到结果;
(2)原式利用平方差公式分解即可;
(3)原式变形后,提取公因式即可得到结果;
(4)原式两项两项结合后,利用平方差公式及提取公因式法分解即可得到结果.
解答 解:(1)原式=a(a-b)3+2a2(a-b)2-2ab(a-b)2=a(a-b)2(a-b+2a-2b)=3a(a-b)3;
(2)原式=(a+2+3a-1)(a+2-3a+1)=(4a+1)(-2a+3);
(3)原式=x4(x-2y)-x2(x-2y)=x2(x-2y)(x2-1)=x2(x-2y)(x+1)(x-1);
(4)原式=(x+y)(x-y)-(x-y)=(x-y)(x+y-1).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
| 捐款金额 | 5元 | 10元 | 15元 | 20元 | 50元 |
| 捐款人数 | 4人 | 12人 | 10 | 18人 | 6人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
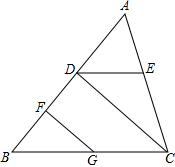 如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.
如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com