
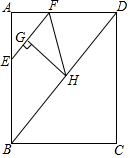
 如图,在矩形ABCD中,AB=8,BC=6,点E从点A出发,以每秒4个单位长度的速度沿边AB运动,到点B停止,过点E作EF∥BD交AD于点F,把△FAE绕点F逆时针方向旋转得到△FGH,点G落在线段EF上,设点E的运动时间为t(秒)
如图,在矩形ABCD中,AB=8,BC=6,点E从点A出发,以每秒4个单位长度的速度沿边AB运动,到点B停止,过点E作EF∥BD交AD于点F,把△FAE绕点F逆时针方向旋转得到△FGH,点G落在线段EF上,设点E的运动时间为t(秒)分析 (1)由△AEF∽△ABD,可得$\frac{AE}{AB}$=$\frac{AF}{AD}$=$\frac{EF}{BD}$,即$\frac{4t}{8}$=$\frac{AF}{6}$=$\frac{EF}{10}$,推出AF=3t,EF=5t,由此即可解决问题.
(2)如图2中,作FN⊥BD于N,GK⊥AB于K,GH交BD于M,连接BG.根据GK=GM列出方程即可解决问题.
(3)分两种情形分别讨论即可①当0<t<$\frac{3}{4}$时,重叠部分是△GFH.②当$\frac{3}{4}$≤t<2时,如图4中,重叠部分是四边形FGMN.
(4)分两种情形分别列出方程即可解决问题.
解答 解:(1)如图1中,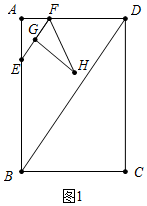
在Rt△ABD中,∵∠A=90°,AB=8,AD=6,
∴BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵EF∥BD,
∴△AEF∽△ABD,
∴$\frac{AE}{AB}$=$\frac{AF}{AD}$=$\frac{EF}{BD}$,
∴$\frac{4t}{8}$=$\frac{AF}{6}$=$\frac{EF}{10}$,
∴AF=3t,EF=5t,
∵AF=FG=3t,
∴EG=EF-FG=2t.
(2)如图2中,作FN⊥BD于N,GK⊥AB于K,GH交BD于M,连接BG.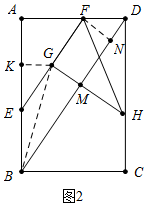
由△GKE∽△FAE,△DFN∽△DBA,可得GK=$\frac{6}{5}$t,FN=GM=$\frac{4}{5}$(6-3t),
∵BG平分∠ABD,
∴GK=GM,
∴$\frac{6}{5}$t=$\frac{4}{5}$(6-3t),
∴t=$\frac{4}{3}$,
∴t=$\frac{4}{3}$时,点G在∠ABD的平分线上.
(3)①如图3中,作AM⊥BD于M,交EF于N.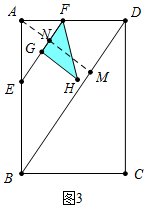
易知AM=$\frac{24}{5}$,AN=$\frac{12}{5}$t,
当点H在BD上时,AN+GH=AM,
∴$\frac{12}{5}$t+4t=$\frac{24}{5}$,
∴t=$\frac{3}{4}$,
当0<t<$\frac{3}{4}$时,重叠部分是△GFH,此时△FGH的周长为y=12t.
②当$\frac{3}{4}$≤t<2时,如图4中,重叠部分是四边形FGMN.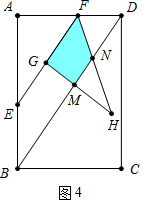
四边形FGMN的周长=y=FG+GF+FH+MN-HM-NH
=12t+$\frac{3}{4}$[4t-($\frac{24}{5}$-$\frac{12}{5}$t)]-[4t-($\frac{24}{5}$-$\frac{12}{5}$t)]-$\frac{5}{4}$[4t-($\frac{24}{5}$-$\frac{12}{5}$t)]=$\frac{12}{5}$t+$\frac{36}{5}$.
综上所述y=$\left\{\begin{array}{l}{12t}&{(0<t<\frac{3}{4})}\\{\frac{12}{5}t+\frac{36}{5}}&{(\frac{3}{4}≤t<2)}\end{array}\right.$.
(4)如图5中,作FN⊥BD于N,设GH交BD于M交CD于K.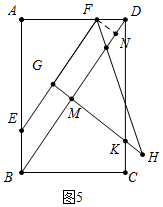
易知DF=6-3t,DN=$\frac{3}{5}$(6-3t),DM=MN+DN=3t+$\frac{3}{5}$(6-3t),DK=$\frac{5}{4}$DM=$\frac{5}{4}$[3t+$\frac{3}{5}$(6-3t)].
由题意9t=10-[3t+$\frac{3}{5}$(6-3t)]或9t-10=$\frac{5}{4}$[3t+$\frac{3}{5}$(6-3t)].
解得t=$\frac{32}{51}$s或$\frac{29}{15}$s.
∴t=$\frac{32}{51}$s或$\frac{29}{15}$s时,点P在直线GH上.
点评 本题考查矩形的性质、旋转变换、角平分线的判定定理、相似三角形的判定和性质,平行线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直平分的四边形是正方形 | |
| B. | 16的平方根是4 | |
| C. | 两边及其一角相等的两个三角形全等 | |
| D. | 数据4,0,4,6,6的方差是4.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
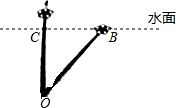 池塘中有一株荷花的茎长为OA,无风时露出水面部分CA=0.4米,如果把这株荷花旁边拉至使它的顶端A恰好到达池塘的水面B处,此时荷花顶端离原来位置的距离BC=1.2米,求这颗荷花的茎长OA.
池塘中有一株荷花的茎长为OA,无风时露出水面部分CA=0.4米,如果把这株荷花旁边拉至使它的顶端A恰好到达池塘的水面B处,此时荷花顶端离原来位置的距离BC=1.2米,求这颗荷花的茎长OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com