【题目】如图，在△ABC中，∠ACB=90°，∠BAC=40°，在直线AC上找点P，使△ABP是等腰三角形，则∠APB的度数为____________．
名校练考卷期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】平行四边形ABCD中，E，F是对角线BD上的两点， 如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（ ）
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在直角坐标系中，反比例函数y＝
(x＞0)，过点A(3，4)．
(1)求y关于x的函数表达式．
(2)求当y≥2时，自变量x的取值范围．
(3)在x轴上有一点P(1，0)，在反比例函数图象上有一个动点Q，以PQ为一边作一个正方形PQRS，当正方形PQRS有两个顶点在坐标轴上时，画出状态图并求出相应S点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
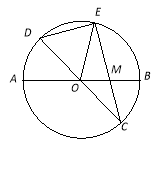
【题目】已知：如图，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连结DE，DE＝
．
（1）求证：
；
（2）求EM的长；
（3）求sin∠EOB的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的，他把这根弹簧的上端固定，在其下端悬挂物体．下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值．
所挂质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 30 | 32 | 34 | 36 | 38 | 40 |
(1)上表所反映的变化过程中的两个变量，________是自变量，________是因变量；
(2)直接写y与x的关系式；
(3)当弹簧长度为130cm(在弹簧承受范围内)时，求所挂重物的质量．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列调查中，适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），AB∥CD，猜想∠BPD与∠B、∠D的关系，说出理由．
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D=180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
（1）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，并说明理由．
（2）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，不需要说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
