
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2+bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3,点P是直线AB下方的抛物线上一动点(不用A,B重合),且点P的横坐标为m,过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2+bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3,点P是直线AB下方的抛物线上一动点(不用A,B重合),且点P的横坐标为m,过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D.分析 (1)根据自变量与函数值的对应关系,可得A,B点,根据待定系数法,可得答案;
(2)①根据平行线的性质,可得∠ACP=∠AEO,根据登记爱噢的正弦函数相等,可得答案;
②根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PC的长,根据正弦函数,可得答案;
(3)根据等底三角形面积的比等于两三角形高的比,可得$\frac{DG}{BF}$,根据面积的比,可得关于m的方程,根据解方程,可得答案.
解答 解:(1)当y=0时,$\frac{1}{2}$x+1=0,解得x=-2,即A(-2,0),
当y=3时,$\frac{1}{2}$x+1=3,解得x=4,即B点坐标为(4,3).
将A,B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{(-2)^{2}a-2b-3=0}\\{{4}^{2}a+4b-3=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{1}{2}$x-3;
(2)①当x=0时,y=$\frac{1}{2}$x+1=1,即E(0,1),
∵PC∥y轴,
∴∠ACP=∠AEO,
∴sin∠ACP=sin∠AEO=$\frac{OA}{AE}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$;
②由点P的横坐标为m,得
P(m,$\frac{1}{2}$m2-$\frac{1}{2}$m-3),C(m,$\frac{1}{2}$m+1),
PC=$\frac{1}{2}$m+1-($\frac{1}{2}$m2-$\frac{1}{2}$m-3)=-$\frac{1}{2}$m2+m+4,
在Rt△PCD中,PD=PC•sin∠ACP=(-$\frac{1}{2}$m2+m+4)×$\frac{2\sqrt{5}}{5}$=-$\frac{\sqrt{5}}{5}$(m2-1)2+$\frac{9\sqrt{5}}{5}$,
∵-$\frac{\sqrt{5}}{5}$<0,
∴当m=1时,PD有最大值$\frac{9\sqrt{5}}{5}$;
(3)存在,
分别过点B,D作BF⊥PC,DG⊥PC,垂足分别为F,G如图 ,
,
在Rt△PDG中,DG=$\frac{1}{\sqrt{5}}$PD=-$\frac{1}{5}$(m2-2m-8),BF=4-m,
$\frac{{S}_{△PCD}}{{S}_{△PCD}}$=$\frac{DG}{BF}$=$\frac{-\frac{1}{5}({m}^{2}-2m-8)}{4-m}$=$\frac{m+2}{5}$,
当$\frac{{S}_{PCD}}{{S}_{△PCB}}$=$\frac{m+2}{5}$=$\frac{9}{10}$时,解得m=$\frac{5}{2}$,
当$\frac{{S}_{△PCD}}{{S}_{△PCB}}$$\frac{m+2}{5}$=$\frac{10}{9}$时,解得m=$\frac{32}{9}$.
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)①的关键是利用等角的正且函数相等;解②得关键是利用平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标得出PC的长,解(3)的关键是利用等底三角形面积的比等于两三角形高的比得出$\frac{DG}{BF}$,要分类讨论,以防遗漏.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
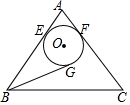 如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.
如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com