
分析 (1)根据题目中数据可以求得按原销售价销售,每天可获得的利润;
(2)根据题目中数据可以求得每套降低10元销售,每天可获得的利润;
(3)①根据题意可以用代数式表示出每套的销售价格;
②根据题意可以用代数式表示出每天的销售量;
③根据题意可以用代数式表示出每天获得的利润;
④根据题意可以得到利润与销售价格之间的关系,从而可以解答本题.
解答 解:(1)按原销售价销售,每天可获利润为:(290-250)×200=8000(元),
故答案为:8000;
(2)若每套降低10元销售,每天可获利润为:(290-10-250)(200+100)=9000(元),
故答案为:9000;
(3)①由题意可得,
每套的销售价格为:(290-10x)元,
故答案为:(290-10x);
②每天可销售:(200+100x)套,
故答案为:(200+100x);
③每天共可以获利润为:(290-10x-250)(200+100x)=(40-10x)(200+100x)元,
故答案为:(40-10x)(200+100x);
④利润为W元,
则W=(40-10x)(200+100x)=-1000(x-1)2+9000,
∴当x=1时,W取得最大值,此时W=9000,
即每套比原销售价降低10元销售,可使每天的获利最大.
点评 本题考查列代数式、求函数的最值,解答此类问题的关键是明确题意,找出所求问题需要的条件,列出相应的代数式,利用二次函数的顶点式求函数的最值.


科目:初中数学 来源: 题型:选择题
| A. | a>0 | B. | a<0 | C. | a>-2 | D. | a<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②均用代入法 | B. | ①②均用加减法 | ||
| C. | ①用代入法,②用加减法 | D. | ①用加减法,②用代入法 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
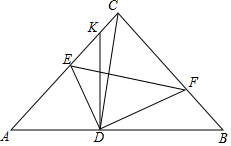 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.
如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
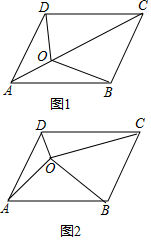 我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形.
我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com