有A,B两个黑袋,A袋中有三个完全相同的小球,分别标有数字-1,0和2,B袋中有三个完全相同的小球,分别标有数字-1,0和2.小明从A袋中随机取出一个小球,将其所标数字记为x,再从B袋中随机取出一个小球,将其所标数字记为y,由此在直角坐标系中确定点P(x,y).
(1)用列表或画树状图的方法写出点P所有可能的坐标;
(2)求点P落在直线y=-x+1上的概率.
分析:(1)首先根据题意画树状图,根据树状图可以求得点P的所有可能坐标;
(2)根据(1)中的树状图,求得点P落在直线y=-x+1上的情况,根据概率公式即可求得答案.
解答:解:(1)画树状图得,
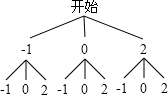
∴点P的坐标有(-1,-1),(-1,0),(-1,2),(0,-1),(0,0),(2,0),(2,-1),(2,0),(2,2);
(2)∵点P落在直线y=-x+1上的有(-1,2),(2,-1),
∴“点P落在直线y=-x+1上”记为事件A,
∴P(A)=
,
即点P落在直线y=-x+1上的概率为
.
点评:本题考查了树状图法与列表法求概率.注意树状图法与列表法可以不重不漏的表示出所有等可能的结果.用到的知识点为:概率=所求情况数与总情况数之比.







