
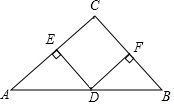
 如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E,F,求证:四边形CEDF是正方形.
如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E,F,求证:四边形CEDF是正方形.  优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
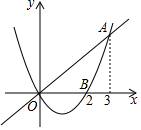 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>3 | C. | 2<x<3 | D. | 0<x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
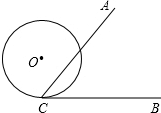 如图,∠ACB=60°,直径为4cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是2$\sqrt{3}$cm.
如图,∠ACB=60°,直径为4cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是2$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
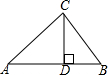 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
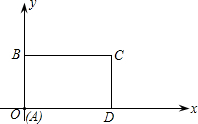 如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
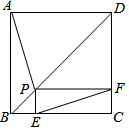 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )| A. | ①②④⑤ | B. | ①②③④⑤ | C. | ①②④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com