
 ,即可求出函数解析式y=-x2+x,继而求出最值.
,即可求出函数解析式y=-x2+x,继而求出最值.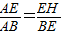 ,又因为△ABE∽△DEH,所以
,又因为△ABE∽△DEH,所以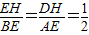 ,即
,即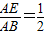 ,所以当E点是AD的中点时,△BEH∽△BAE.
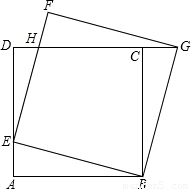
,所以当E点是AD的中点时,△BEH∽△BAE.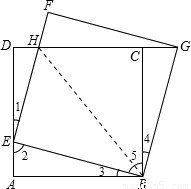 解:(1)AE=CG.
解:(1)AE=CG.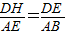 .
.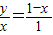 .
. )2+
)2+
 时,y有最大值为
时,y有最大值为 .
. .
. .
.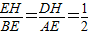 .
. ,
,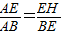 .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:2010年浙江省宁波市余姚中学自主招生考试数学试卷(解析版) 题型:解答题
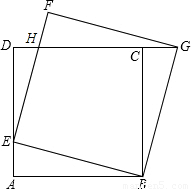
查看答案和解析>>
科目:初中数学 来源:2010年广东省湛江市初中毕业生学业水平综合测试数学试卷(一)(解析版) 题型:解答题
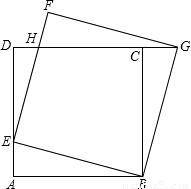
查看答案和解析>>
科目:初中数学 来源:2006年福建省南平市中考数学试卷(解析版) 题型:解答题
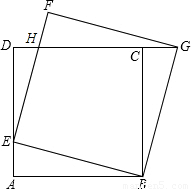
查看答案和解析>>
科目:初中数学 来源:2009年江苏省苏州市张家港市中考数学模拟练习试卷(2)(解析版) 题型:解答题
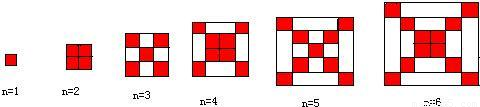
| 正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
| 红色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
| 红色小正方形个数 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com