
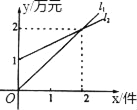
【题目】如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
(1)x=1时,销售收入= 万元,销售成本= 万元,盈利(收入﹣成本)= 万元;
(2)一天销售 件时,销售收入等于销售成本;
(3)l2对应的函数表达式是 ;
(4)你能写出利润与销售量间的函数表达式吗?
【答案】(1)1,![]()
【解析】
(1)根据线段中点的求法列式计算即可求出x=1时的销售收入和销售成本,根据盈利的求法计算即可得解;
(2)根据图象找出两直线的交点的横坐标即可;
(3)设l2对应的函数表达式为y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答;
(4)再写出l1的解析式,然后根据利润=销售收入-销售成本列式整理即可.
(1)x=1时,销售收入![]() 万元,销售成本
万元,销售成本![]() 万元,盈利(收入成本)
万元,盈利(收入成本)![]() 万元;
万元;
(2)一天销售2件时,销售收入等于销售成本;
(3)设l2对应的函数表达式为y=kx+b(k≠0),
∵函数图象经过点(0,1),(2,2),
∴![]()
解得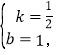
∴l2对应的函数表达式是![]()
(4)∵l1经过原点和(2,2),
∴l1的表达式为y=x,
∴利润![]()
故答案为:(1) 1,![]()


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
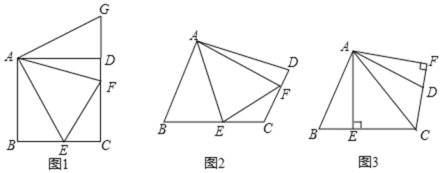
【题目】(1)如图 1,四边形 ABCD 中,∠BAD=∠ADC=∠CBA=90°,AB=AD,点 E、F 分别在四边形 ABCD 的边 BC、CD 上,∠EAF=45°,点 G 在 CD 的延长线上,BE=DG,连接 AG,求证:EF=BE+FD.
(2)如图 2,四边形 ABCD 中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点 E、F 分别在边BC、CD 上,则当∠BAD=2∠EAF 时,仍有 EF=BE+FD 成立吗?说明理由.
(3)如图 3,四边形 ABCD 中,∠BAD≠90°,AB=AD,AC 平分∠BCD,AE⊥BC 于 E,AF⊥CD 交 CD 延长线于 F,若 BC=9,CD=4,则 CE= .(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形: 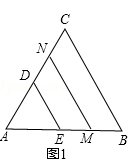
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由; 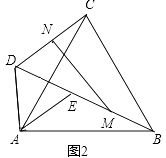
(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至点A′的位置,使点A与点A′对应,画出平移后得到的△A′B′C′;
(2)△A′B′C′可以看成是把△ABC如何平移得到的?
(3)写出图中与线段AA′平行且相等的线段(可用字母表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
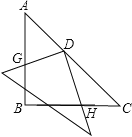
【题目】如图所示:一副三角板如图放置,等腰直角三角板ABC固定不动,另一块三角板的直角顶点放在等腰直角三角形的斜边中点D处,且可以绕点D旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.
![]() 在旋转过程中线段BG和CH大小有何关系?证明你的结论.
在旋转过程中线段BG和CH大小有何关系?证明你的结论.
![]() 若
若![]() ,在旋转过程中四边形GBHD的面积是否改变?若不变,求出它的值;若改变,求出它的取值范围.
,在旋转过程中四边形GBHD的面积是否改变?若不变,求出它的值;若改变,求出它的取值范围.
![]() 若交点G、H分别在边AB、BC的延长线上,则
若交点G、H分别在边AB、BC的延长线上,则![]() 中的结论仍然成立吗?请画出相应的图形,直接写出结论.
中的结论仍然成立吗?请画出相应的图形,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由(根据解题的要求,在横线处或括号内填写适当的内容或理由).
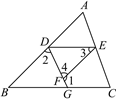
解:∠AED=∠C.
理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,∴AB∥EF,
∴________________(两直线平行,内错角相等).
又∵∠3=∠B,∴∠B=∠ADE,
∴DE∥BC(____________________________),
∴∠AED=∠C(__________________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com