
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )
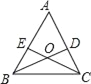
A. 5对 B. 6对 C. 7对 D. 8对
【答案】C
【解析】
题中相等的角有:∠ABC=∠ACB、∠ADB=∠AEC=90°、∠BOE=∠COD、∠EAC=∠DAB,根据这些相等角可得出的相似三角形有:
△ADB∽△AEC(∠A=∠A,∠ADB=∠AEC);
△BEC∽△CDB(∠BEC=∠CDB,∠ABC=∠ACB);
△BOE∽△COD(∠BEC=∠CDB,∠BOE=∠COD);
△COD∽△CAE(∠ACE=∠OCD,∠CDO=∠CEA);
同理可证得:△BOE∽△BAD、△BOE∽△CAE、△COD∽△BAD;
∵在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高;
∴∠ABC=∠ACB,∠BEC=∠CDB=90°
∴△BEC∽△CDB
∵∠EOB=∠DOC,∠BEC=∠CDB=90°
∴△BEO∽△CDO
∵∠ABD=∠ABD,∠BEO=∠BDA=90°
∴△BEO∽△BDA
同理△CDO∽△CEA;
∵∠A=∠A,∠AEC=∠ADB=90°
∴△AEC∽△ADB
∴共有7对相似三角形.
故选C.


科目:初中数学 来源: 题型:
【题目】小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。
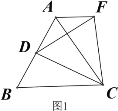
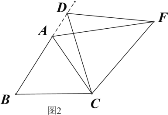
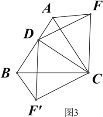

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.

(1)求点B的坐标;
(2)在x轴上找一点D,连接BD使得△ABD与△ABC相似(不包括全等),并求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中,AB=AC,∠BAC=120,
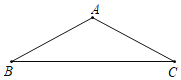
(1)利用直尺、圆规,求作AB的垂直平分线DE,交BC于点D、交AB于点E:(不要求写出作法,但要求保留作图痕迹)
(2)若BD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点P是BC延长线上一点,连结PD并延长交BA延长线于点E.记△ABP的面积为S1,△ECP的面积为S2,则S1与S2的大小关系是( )
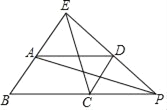
A. S1=S2 B. S1>S2 C. S1<S2 D. 都可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB = 30°,点P是∠AOB内任意一点,且OP = 7,点E和点F分别是射线OA和射线OB上的动点,则△PEF周长的最小值是______.
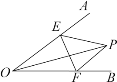
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC中,BC=AC,∠ACB=90°,将该三角形在直角坐标系中放置.

(1)如图(1),过点A作AD⊥x轴,当B点为(0,1),C点为(3,0)时,求OD的长;
(2)如图(2),将斜边顶点A、B分别落在y轴上、x轴上,若A点为(0,1),B点为(4,0),求C点坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com