
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.深圳市环境卫生局为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
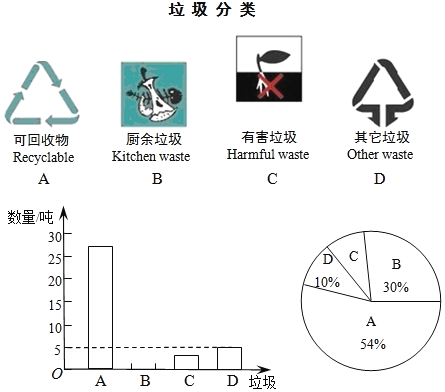
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,产生的有害垃圾C所对应的圆心角为 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设深圳市每天产生的生活垃圾为28500吨,且全部分类处理,那么每天回收的塑料类垃圾可以获得多少吨二级原料?
【答案】(1)见解析;(2)21.6;(3)1000.35吨
【解析】
(1)根据统计图中D类垃圾的吨数和所占的百分比,可以求得本次调查的垃圾总数,然后即可得到B类垃圾的吨数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据,可以得到在扇形统计图中,产生的有害垃圾C所对应的圆心角的度数;
(3)根据题意和统计图中的数据,可以计算出每天回收的塑料类垃圾可以获得多少吨二级原料
解:(1)本次调查的吨数为:5÷10%=50,
B类有50×30%=15(吨),
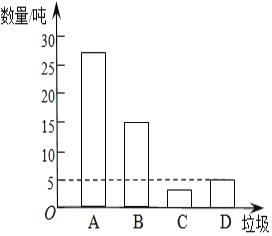
补全的条形统计图如右图所示;
(2)在扇形统计图中,产生的有害垃圾C所对应的圆心角为:360°×(1﹣54%﹣30%﹣10%)=21.6°,
故答案为:21.6;
(3)28500×54%×13%×0.5=1000.35(吨),
答:每天回收的塑料类垃圾可以获得1000.35吨二级原料.


科目:初中数学 来源: 题型:
【题目】初三年级教师对试卷讲评课中学生参与的深度和广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
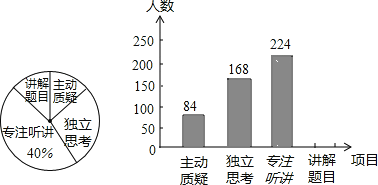
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有12000名初中学生,那么在试卷讲评课中,独立思考的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
餐食种类 | 价格(单位:元) |
汉堡套餐 | 40 |
鸡翅 | 16 |
鸡块 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花____________元(含送餐费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 是
是![]() 上的定点,点
上的定点,点![]() 为优弧
为优弧![]() 上的动点(不与点
上的动点(不与点![]() ,
,![]() 重合),在点
重合),在点![]() 运动的过程中,以下结论正确的是( )
运动的过程中,以下结论正确的是( )

A.![]() 的大小改变B.点
的大小改变B.点![]() 到弦
到弦![]() 所在直线的距离存在最大值
所在直线的距离存在最大值
C.线段![]() 与
与![]() 的长度之和不变D.图中阴影部分的面积不变
的长度之和不变D.图中阴影部分的面积不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转45°,得到
顺时针旋转45°,得到![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)根据题意补全图形;
(2)判断![]() 的形状,并证明;
的形状,并证明;
(3)连接![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.
解法1的主要思路:
延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,可证
,可证![]() ,再证
,再证![]() 是等腰直角三角形.
是等腰直角三角形.
解法2的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,可证
,可证![]() 是等腰直角三角形,再证
是等腰直角三角形,再证![]() .
.
解法3的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,用含
,用含![]() 或
或![]() 的式子表示
的式子表示![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
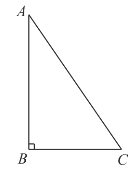
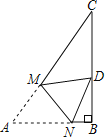
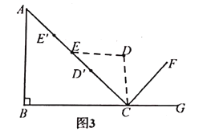
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
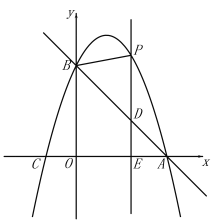
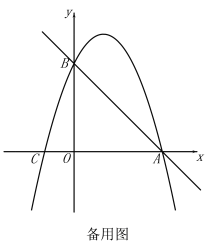
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
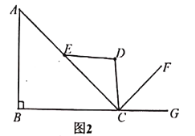
【题目】如图1所示的健身器械为倒蹬机,使用方法为上身不动,腿部向前发力,双腿伸直之后,然后再慢慢回收.图2为示意图,已知![]() 在初始位置,
在初始位置,![]() , 点
, 点![]() 在同一直线上,
在同一直线上,![]() .
.

(1)当![]() 在初始位置时,求点
在初始位置时,求点![]() 到
到![]() 的距离;
的距离;
(2)当双腿伸直后,如图3,点![]() 分别从初始位置运动到点
分别从初始位置运动到点![]() , 假设
, 假设![]() 三点共线,求此时点
三点共线,求此时点![]() 上升的竖直高度. ( 结果精确到个位) (参考数据:
上升的竖直高度. ( 结果精确到个位) (参考数据:![]()
![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
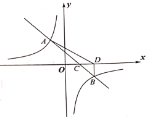
【题目】一次函数![]() 的图像与双曲线
的图像与双曲线![]()
![]() 相交于
相交于![]() 和
和![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求一次函数的解析式;
(2)根据图像直接写出不等式![]() 的解集;
的解集;
(3)![]() 的面积为
的面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com