
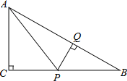
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上不同于
边上不同于![]() 、
、![]() 的一动点,过
的一动点,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
![]() 试说明不论点
试说明不论点![]() 在
在![]() 边上何处时,都有
边上何处时,都有![]() 与
与![]() 相似;
相似;
![]() 若
若![]() ,
,![]() ,当
,当![]() 为何值时,
为何值时,![]() 面积最大,并求出最大值;
面积最大,并求出最大值;
![]() 在
在![]() 中,两条直角边
中,两条直角边![]() 、
、![]() 满足关系式
满足关系式![]() ,是否存在一个
,是否存在一个![]() 的值,使
的值,使![]() 既与
既与![]() 全等,也与
全等,也与![]() 全等.
全等.
科目:初中数学 来源: 题型:
【题目】有个均匀的正十二面体的骰子,其中1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,1个面标有“5”,其余面标有“6”,将这个骰子掷出后:
(1)掷出“6”朝上的可能性有多大?
(2)哪些数字朝上的可能性一样大?
(3)哪些数字朝上的可能性最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为P(2,9),与x轴交于点A,B,与y轴交于点C(0,5).
(Ⅰ)求二次函数的解析式及点A,B的坐标;
(Ⅱ)设点Q在第一象限的抛物线上,若其关于原点的对称点Q′也在抛物线上,求点Q的坐标;
(Ⅲ)若点M在抛物线上,点N在抛物线的对称轴上,使得以A,C,M,N为顶点的四边形是平行四边形,且AC为其一边,求点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
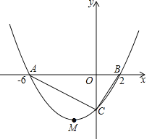
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 为
为![]() 三条角平分线的交点,
三条角平分线的交点,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离为( )
的距离为( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com