
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当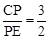 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.
解:(1)证明:∵AP′是AP旋转得到,∴AP=AP′。∴∠APP′=∠AP′P。
∵∠C=90°,AP′⊥AB,∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°。
又∵∠BPC=∠APP′(对顶角相等)。∴∠CBP=∠ABP。
(2)证明:如图,过点P作PD⊥AB于D,
∵∠CBP=∠ABP,∠C=90°,∴CP=DP。
∵P′E⊥AC,∴∠EAP′+∠AP′E=90°。
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E。
在△APD和△P′AE中,
∵ ,
,
∴△APD≌△P′AE(AAS)。∴AE=DP。∴AE=CP。
(3)∵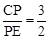 ,∴设CP=3k,PE=2k,则AE=CP=3k,AP′=AP=3k+2k=5k。
,∴设CP=3k,PE=2k,则AE=CP=3k,AP′=AP=3k+2k=5k。
在Rt△AEP′中, ,
,
∵∠C=90°,P′E⊥AC,∴∠CBP+∠BPC=90°,∠EP′P+∠P′PE=90°。
∵∠BPC=∠EPP′(对顶角相等),∴∠CBP=∠P′PE。
又∵∠BAP′=∠P′EP=90°,∴△ABP′∽△EPP′。
∴ 。即
。即 。∴
。∴ 。
。
在Rt△ABP′中, ,即
,即 。
。
解得AB=10
解析试题分析:(1)根据旋转的性质可得AP=AP′,根据等边对等角的性质可得∠APP′=∠AP′P,再根据等角的余角相等证明即可。
(2)过点P作PD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CP=DP,然后求出∠PAD=∠AP′E,利用“角角边”证明△APD和△P′AE全等,根据全等三角形对应边相等可得AE=DP,从而得证。
(3)设CP=3k,PE=2k,表示出AE=CP=3k,AP′=AP=5k,然后利用勾股定理列式求出P′E=4k,再求出△ABP′和△EPP′相似,根据相似三角形对应边成比例列式求出 ,然后在Rt△ABP′中,利用勾股定理列式求解即可。
,然后在Rt△ABP′中,利用勾股定理列式求解即可。


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B?A,B?C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.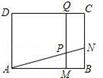
(1)若a=4厘米,t=1秒,则PM= _________ 厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN,梯形PQDA,梯形PQCN的面积都相等?若存在,求a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡角 为
为 ,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.
,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.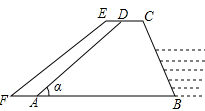
(1)求完成该工程需要多少立方米方土?
(2)某工程队在加固600立方米土后,采用新的加固模式,这样每天加固方数是原来的2倍,结果只用11天完成了大坝加固的任务.请你求出该工程队原来每天加固多少立方米土?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF .
.
图1
(1)求 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: ;
;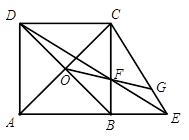
图2
(3)在(2)的条件下,当 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
① 分别求出直线l与双曲线的解析式;(3分)
② 若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?(4分)
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.(2分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
“横看成岭侧成峰”从数学的角度解释为( )
| A.从不同的方向观察同一建筑物时,看到的图形不一样 |
| B.从同一方向观察同一建筑物时,看到的图形不一样 |
| C.从同一的方向观察不同的建筑物时,看到的图形一样 |
| D.以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com