
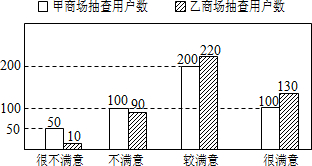
 如图反映了被调查用户对甲,乙两种品牌空调售后服务的满意程度(以下称:用户满意度),分为很不满意,不满意,较满意,很满意,四个等级,并依次记为1分,2分,3分,4分.
如图反映了被调查用户对甲,乙两种品牌空调售后服务的满意程度(以下称:用户满意度),分为很不满意,不满意,较满意,很满意,四个等级,并依次记为1分,2分,3分,4分. 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
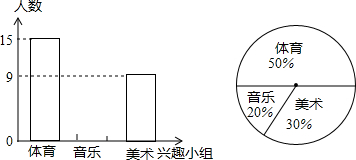
| A. | 八年级(1)班参加这三个课外兴趣小组的学生总人数为30人 | |
| B. | 在扇形统计图中,八年级(1)班参加音乐兴趣小组的学生人数所占的圆心角度数为82° | |
| C. | 八年级(1)班参加音乐兴趣小组的学生人数为6人 | |
| D. | 若该校八年级参加这三个兴趣小组的学生共有200人,那么估计全年级参加美术兴趣小组的学生约有60人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com