
分析 (1)根据“利润=(售价-成本)×销售量”列出方程;
(2)每天的销售利润不低于4000元,根据二次函数与不等式的关系求出x的取值范围,再根据每天的总成本不超过7000元,以及50≤x≤100,列不等式组即可.
解答 解:(1)y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500,
所以y=-5x2+800x-27500(50≤x≤100);
(2)当y=4000时,-5(x-80)2+4500=4000,
解得:x1=70,x2=90,
∴当70≤x≤90时,每天的销售利润不低于4000元,
由每天的总成本不超过7000元,得50(-5x+550)≤7000,解得:x≥82,
∴82≤x≤90,
∵50≤x≤100,
∴销售单价应该控制在82元至90元之间.
点评 本题主要考查二次函数的实际应用.数学建模题,借助二次函数解决实际问题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:填空题
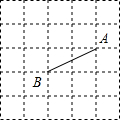 如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知Rt△ABC中,∠ACB=90°,以BC为直径作⊙O交AB于点D,E是AC上一点,且DE=CE,连接OE.
如图,已知Rt△ABC中,∠ACB=90°,以BC为直径作⊙O交AB于点D,E是AC上一点,且DE=CE,连接OE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com