
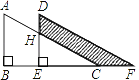
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
科目:初中数学 来源: 题型:
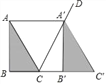
【题目】如图,将△ABC沿着射线BC方向平移至△A′B′C′,使点A′落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A′的形状,并说明理由;
(2)在△ABC中,∠B=90°,AB=8,cos∠BAC=![]() ,求CB′的长.
,求CB′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股票经纪人给他的投资者出了一道题,说明投资人的赢利净赚情况(单位:元):
股票名称 | 中国重工 | 五粮液 | 工商银行 | 四川路桥 |
每股净赚(元) | +23 | +1.5 | ﹣3 | ﹣(﹣2) |
股数 | 500 | 1000 | 1000 | 500 |
请你计算一下,投资者到底是赔了还是赚了,赔了或赚了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
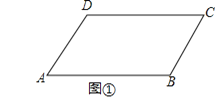
【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=![]() ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
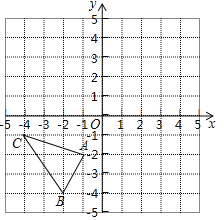
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com