
分析 首先根据$\frac{1}{2}=\frac{4}{8}$,$\frac{2}{7}$=$\frac{4}{14}$,可得当这列数的分子都化成4时,分母分别是5、8、11、14、…,分母构成以5为首项,以3为公差的等差数列,据此求出这列数中的第10个数与第16个数各是多少;然后求出它们的积是多少即可.
解答 方法一:
解:∵$\frac{1}{2}=\frac{4}{8}$,$\frac{2}{7}$=$\frac{4}{14}$,
∴这列数依次为:$\frac{4}{5}$,$\frac{4}{8}$,$\frac{4}{11}$,$\frac{4}{14}$,…,
∴当这列数的分子都化成4时,分母分别是5、8、11、14、…,
∵8-5=11-8=14-11=3,
∴分母构成以5为首项,以3为公差的等差数列,
∴这列数中的第10个数与第16个数的积是:
$\frac{4}{5+(10-1)×3}×\frac{4}{5+(16-1)×3}$
=$\frac{1}{8}×$$\frac{2}{25}$
=$\frac{1}{100}$.
故答案为:$\frac{1}{100}$.
方法二:
将$\frac{4}{5}$,$\frac{1}{2}$,$\frac{4}{11}$,$\frac{2}{7}$化成分子相同的形式$\frac{4}{5}$,$\frac{4}{8}$,$\frac{4}{11}$,$\frac{4}{14}$,
经观察,此数列分母为一阶等差,
∴设s=kn+b,
$\left\{\begin{array}{l}{k+b=5}\\{2k+b=8}\end{array}\right.$,
∴k=3,b=2,
∴s=3n+2,
∴s10=$\frac{4}{32}$,s16=$\frac{4}{50}$,
∴s10×s16=$\frac{1}{100}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:当这列数的分子都化成4时,分母构成以5为首项,以3为公差的等差数列.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题

| A. | -20m | B. | 10m | C. | 20m | D. | -10m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
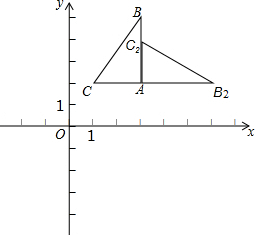 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
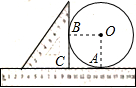 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 | ||
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com