
【题目】《雁栖塔》位于怀柔“北京雁栖湖国际会都中心”所处大岛西南部突出部位的半岛上,是“北京雁栖湖国际会都中心”的标志性建筑,也是整个雁栖湖风景区的标志性建筑. 某校数学课外小组为了测量《雁栖塔》(底部可到达)的高度,准备了如下的测量工具:①平面镜,②皮尺,③长为1米的标杆,④高为1.5m的测角仪(测量仰角、俯角的仪器).第一组选择用②④做测量工具;第二组选用②③做测量工具;第三组利用自身的高度并选用①②做测量工具,分别画出如下三种测量方案示意图.
(1)请你判断如下测量方案示意图各是哪个小组的,在测量方案示意图下方的括号内填上小组名称.
(2)选择其中一个测量方案示意图,写出求《雁栖塔》高度的思路.
【答案】
(1)解:二组 一组 三组
(2)解:一图思路:①分别测出在同一时刻标杆EF和《雁栖塔》AB的影长DF,CB;
②由△ABC∽△EFD,利用 ![]() 求出AB的值,
求出AB的值,
二图思路:①用测角仪测出∠ACB的角度; ②用皮尺测量CB的长;
③AB=CBtan∠ACB; ④AE=AB+1.5,
三图思路:①用皮尺分别测量DF、CF、CB的长;
②由△ABC∽△DFE,利用 ![]() 求出AB的值
求出AB的值
【解析】(1)根据题意即可得到结论;(2)一图思路:分别测出在同一时刻标杆EF和《雁栖塔》AB的影长DF,CB;根据相似三角形的性质即可得到结论;二图思路:用测角仪测出∠ACB的角度; 用皮尺测量CB的长;解直角三角形即可得到快乐;三图思路:用皮尺分别测量DF、CF、CB的长;根据相似三角形的性质即可得到结论.
【考点精析】关于本题考查的相似三角形的应用和关于仰角俯角问题,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF. 
(1)求证:EF∥平ABD面;
(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E. 请问:△CDP与△PAE相似吗?如果相似,请写出证明过程.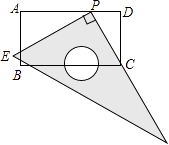
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③ ![]() .其中正确的有( )
.其中正确的有( ) 
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( ) 
A.1月份
B.2月份
C.5月份
D.7月份
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.
(1)如图(1),当点E在BC边的中点位置时,通过测量AE,EM的长度,猜想AE与EM满足的数量关系是;
(2)如图(2),小晏通过观察、实验,提出猜想:当点E在BC边的任意位置时,始终有AE=EM.小晏把这个猜想与同学进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:在BA上取一点H使AH=CE,连接EH,要证AE=EM,只需证△AHE≌△ECM.
想法2:找点A关于直线BC的对称点F,连接AF,CF,EF.(易证∠BCF+∠BCA+ACM=180°,所以M,C,F三点在同一直线上)要证AE=EM,只需证△MEF为等腰三角形.
想法3:将线段BE绕点B顺时针旋转60°,得到线段BF,连接CF,EF,要证AE=EM,只需证四边形MCFE为平行四边形.
请你参考上面的想法,帮助小晏证明AE=EM.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点. 
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里) (参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)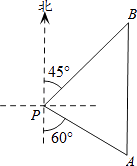
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论: ①4a+b=0;
②9a+c<3b;
③25a+5b+c=0;
④当x>2时,y随x的增大而减小.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com