
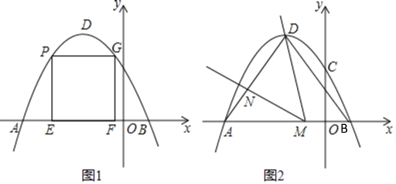
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0).
x2+bx+c经过点A(﹣5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A、D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G,过点G作GF⊥x轴于点F,当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD、BD,点M在线段AB上(不与A、B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
【答案】(1)抛物线的表达式为:y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,D(﹣2,4);(2)点P的横坐标为﹣
,D(﹣2,4);(2)点P的横坐标为﹣![]() ;(3)AN=1或
;(3)AN=1或![]() .
.
【解析】
(1)根据抛物线过A、B两点,可用交点式求出抛物线的解析式,然后求抛物线的顶点坐标即可;
(2)设点P(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),分别用m表示出PE和PG,从而得出矩形的周长与m的二次函数关系式,利用二次函数的顶点式求最值即可;
),分别用m表示出PE和PG,从而得出矩形的周长与m的二次函数关系式,利用二次函数的顶点式求最值即可;
(3)利用相似三角形的判定定理可得△BDM∽△AMN,列出比例式,并根据平面直角坐标系中任意两点之间的距离公式分别求出AB、AD、BD,最后根据等腰三角形的腰的情况分类讨论即可.
解:(1)∵抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0)
x2+bx+c经过点A(﹣5,0)和点B(1,0)
∴抛物线的表达式为:y=﹣![]() (x+5)(x﹣1)=﹣
(x+5)(x﹣1)=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
则顶点坐标的横坐标为: 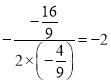 ,代入可得顶点坐标的纵坐标为:4
,代入可得顶点坐标的纵坐标为:4
∴点D(﹣2,4);
(2)设点P(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),
),
则PE=﹣![]() m2﹣
m2﹣![]() m+
m+![]() ,PG=2(﹣2﹣m)=﹣4﹣2m,
,PG=2(﹣2﹣m)=﹣4﹣2m,
∴矩形PEFG的周长=2(PE+PG)=2(﹣![]() m2﹣
m2﹣![]() m+
m+![]() ﹣4﹣2m)=﹣
﹣4﹣2m)=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵﹣![]() <0,故当m=﹣
<0,故当m=﹣![]() 时,矩形PEFG周长最大,
时,矩形PEFG周长最大,
此时,点P的横坐标为﹣![]() ;
;
(3)∵∠DMN=∠DBA,
∠BMD+∠BDM=180°﹣∠ADB,
∠NMA+∠DMB=180°﹣∠DMN,
∴∠NMA=∠MDB,
∴△BDM∽△AMN,
∴![]() ,
,
而AB=1-(﹣5)=6,AD=BD=![]() =5,
=5,
①当MN=DM时,
∴△BDM≌△AMN,
即:AM=BD=5,则AN=MB=AB-AM=1;
②当NM=DN时,
则∠NDM=∠NMD,
∴△AMD∽△ADB,
∴AD2=AB×AM,即:25=6×AM,则AM=![]() ,
,
而![]() ,即
,即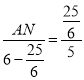 ,
,
解得:AN=![]() ;
;
③当DN=DM时,
∵∠DNM>∠DAB,而∠DAB=∠DMN,
∴∠DNM>∠DMN,
∴DN≠DM;
综上所述:AN=1或![]() .
.


科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
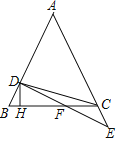
【题目】如图,在△ABC中,AB=AC,点D在AB上,点E在AC延长线上,且BD=CE,连接DE交BC于点F,作DH⊥BC于点H,连接CD.若tan∠DFH=![]() ,S△BCD=18,则DE的长为_____.
,S△BCD=18,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
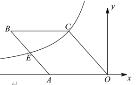
【题目】如图,在平面直角坐标系中,菱形 ABCO 的一边 OA 在 x 轴上,![]() ,反比例函数
,反比例函数![]() 过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
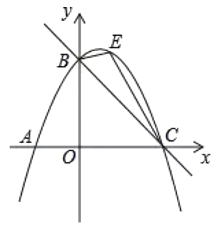
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱![]() 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
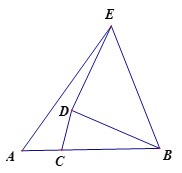
【题目】如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 ________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com