
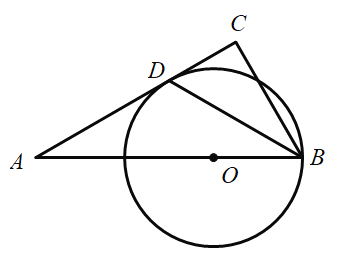
【题目】如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半轻的⊙O与AC相切于点D,BD平分∠ABC,∠ABC=60°.
(1)求∠C的度数;
(2)若圆的半径OB=2,求线段CD的长度.
【答案】(1)∠C=90°;(2) CD=![]()
【解析】
(1)连接OD,∠ADO=90°,由BD平分∠ABC,OB=OD可得OD ∥BC,则∠ACB=90°;
(2)得Rt△OAD,由∠ABC=∠AOD =60°,OD=2,可求出AD、AO的长;根据平行线分线段成比例定理,得结论.
(1)如图,连接OD

∵OD是⊙O的半径,AC是⊙O的切线,点D是切点,
∴OD⊥AC
∵OD=OB,
∴∠ODB=∠OBD,
又∵BD平分∠ABC,
∴∠OBD=∠CBD
∴∠ODB=∠CBD
∴OD∥CB,
∴∠C=∠ADO=90°;
(2)在Rt△AOD中,∵∠ABC=∠AOD =60°,OD=2,
∴AD=2![]() ,AO=4,
,AO=4,
∵OD∥CB,
∴![]() ,
,
即![]() ,
,
∴CD=![]() .
.


科目:初中数学 来源: 题型:
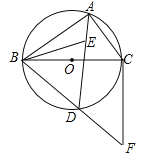
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
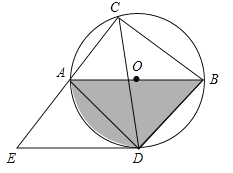
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的曲边三角形的面积是 ;
围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
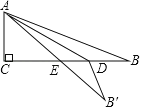
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线AB的解析式为y=﹣![]() x+4,抛物线y=﹣
x+4,抛物线y=﹣![]() +bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.
+bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.
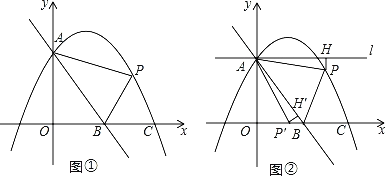
(1)求抛物线的解析式;
(2)当点P在第一象限内时,求△ABP面积的最大值,并求此时点P的坐标;
(3)如图②,当点P在y轴右侧时,过点A作直线l∥x轴,过点P作PH⊥l于点H,将△APH绕点A顺时针旋转,当点H的对应点H′恰好落在直线AB上时,点P的对应点P′恰好落在坐标轴上,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18![]() m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )

A.55.5mB.54mC.19.5mD.18m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣
x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
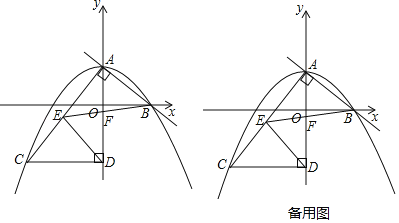
(1)求抛物线的表达式;
(2)求点C的坐标;
(3)若点G在直线AB上,连接FG,当∠AGF=∠AFB时,直接写出线段AG的长;
(4)在(3)的条件下,点H在线段ED上,点P在平面内,当△PAG≌△PDH时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
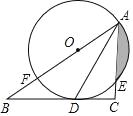
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P'是边AB上一点,四边形P'Q'M'N'是正方形,点Q',![]() 在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
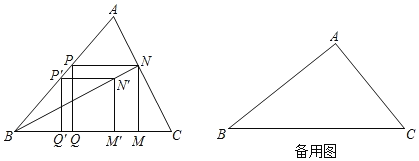
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com