
【题目】在ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD= .
【答案】![]() 或5
或5
【解析】解:分两种情况:①如图1,
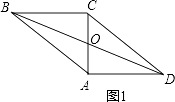
∵△ABC是直角三角形,
∠ACB=90°,AB=4,AC=3,
∴BC2=AB2﹣AC2=42﹣32=7.
∴AD=BC= ![]() ;②如图2,
;②如图2,
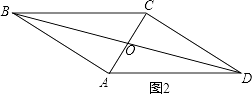
∵ABCD的对角线AC与BD相交于点O,
∴BD=2BO,OC=OA= ![]() AC,
AC,
∵∠BAC=90°,AB=4,AC=3,
∴BC2=AB2+AC2=16+9=25,
∴BC=5,
∴AD=5;
所以答案是: ![]() 或5.
或5.
【考点精析】根据题目的已知条件,利用勾股定理的概念和平行四边形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确的结论有( )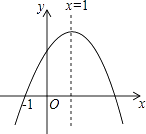
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因为![]() ,所以
,所以![]() .这说明
.这说明![]() 能被
能被![]() 整除,同时也说明多项式
整除,同时也说明多项式![]() 有一个因式为
有一个因式为![]() ;另外,当
;另外,当![]() 多项式
多项式![]() 的值为
的值为![]() .阅读上述材料回答问题:
.阅读上述材料回答问题:
(1)由![]() 可知,当
可知,当![]() _时,多项式
_时,多项式![]() 的值为
的值为![]() ;
;
(2)一般地,如果一个关于字母![]() 的多项式
的多项式![]() 当
当![]() 时,
时,![]() 的值为
的值为![]() ,那么
,那么![]() 与代数式
与代数式![]() 之间有一定的关系,这种关系是:_____;
之间有一定的关系,这种关系是:_____;
(3)已知关于![]() 的多项式
的多项式![]() 能被
能被![]() 整除,试求
整除,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题: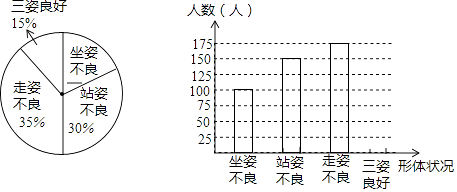
(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;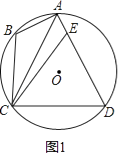
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;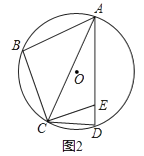
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= ![]() ,EG=2,求AE的长.
,EG=2,求AE的长.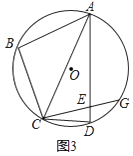
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.
(1)在图1中确定点C(点C在小正方形的顶点上),要求以A、B、C为顶点的三角形为锐角等腰三角形,画出此三角形(画出一个即可);
(2)在图2中确定点D(点D在小正方形的顶点上),要求以A、B、D为顶点的三角形是以AB为斜边的直角三角形,画出此三角形(画出一个即可),并直接写出此三角形的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如:a=12,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为3311=3,所以f(12)=3.
根据以上定义,回答下列问题:
(1)填空:
①下列两位数:40,42,44中,“迥异数”为 ;
②计算:f(23)= .
(2)如果一个“迥异数”b的十位数字是k,个位数字是2(k+1),且f(b)=11,请求出“迥异数”b.
(3)如果一个“迥异数”c,满足c5f(c)30,请直接写出满足条件的c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com