
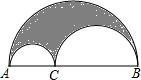
 如图,以AB为直径画一个大半圆,BC=2AC,分别以AC,CB为直径在大半圆内部画两个小半圆,那么阴影部分的面积与大半圆面积的比等于________.
如图,以AB为直径画一个大半圆,BC=2AC,分别以AC,CB为直径在大半圆内部画两个小半圆,那么阴影部分的面积与大半圆面积的比等于________. 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
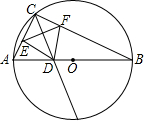 聪聪同学从小就喜欢动手动脑,请看他的研究:
聪聪同学从小就喜欢动手动脑,请看他的研究:查看答案和解析>>
科目:初中数学 来源: 题型:
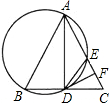 如图,已知△ABC中,AB=AC,以AB为直径画圆,交BC于D,交AC于E,过D作DF⊥CE,垂足为F.由上述条件(不另增字母或添线),请你写出三个你认为是正确的结论(不要求证明).
如图,已知△ABC中,AB=AC,以AB为直径画圆,交BC于D,交AC于E,过D作DF⊥CE,垂足为F.由上述条件(不另增字母或添线),请你写出三个你认为是正确的结论(不要求证明).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com