
【题目】如图,点![]() 是
是![]() 直径
直径![]() 上一点,过
上一点,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() .
.
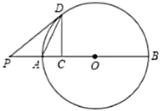
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析 (2)BC=12
【解析】
(1)求出∠ODA+∠PDA=∠ADC+∠DAO=90°,根据切线的判定得出即可;
(2)连接OD,求出∠PDC=∠DOC,解直角三角形求出![]() ,设DC=4x,OC=3x,求出3x+3=5x,求出x,即可得出答案.
,设DC=4x,OC=3x,求出3x+3=5x,求出x,即可得出答案.
(1)证明:连接OD,

∵OD=OA,
∴∠ODA=∠OAD,
∵CD⊥AB于点C,
∴∠OAD+∠ADC=90°,
∴∠ODA+∠ADC=90°,
∵∠PDA=∠ADC,
∴∠PDA+∠ODA=90°,
即∠PDO=90°,
∴PD⊥OD,
∵D在⊙O上,
∴PD是⊙O的切线;
(2) ∵∠PDO=90°,
∴∠PDC+∠CDO=90°,
∵CD⊥AB于点C,
∴∠DOC+∠CDO=90°,
∴∠PDC=∠DOC,
∵tan∠PDC=![]() ,
,
∴tan∠DOC=![]() =
=![]()
设DC=4x,CO=3x,则OD=5x,
∵AC=3,
∴OA=3x+3,
∴3x+3=5x,
∴x=![]()
∴OC=3x=![]()
OD=OB=5x=![]()
∴BC=12.


科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC,BC,AD,BD,且AD与BC相交于点F,延长AC至E,使AC=EC,连接EB交AD的延长线于点G.
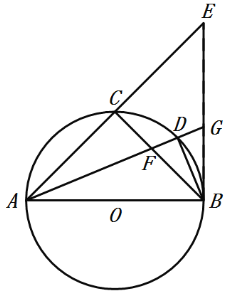
(1)求证:EB是⊙O的切线;
(2)求证;AF=2BD;
(3)求证:线段BG是线段CF和线段EG的比例中项.
查看答案和解析>>
科目:初中数学 来源: 题型:
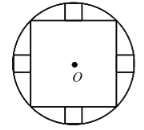
【题目】如图,圆形纸片⊙O半径为 5![]() ,先在其内剪出一个最大正方形,再在剩余部分剪出 4个最大的小正方形,则 4 个小正方形的面积和为_______.
,先在其内剪出一个最大正方形,再在剩余部分剪出 4个最大的小正方形,则 4 个小正方形的面积和为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
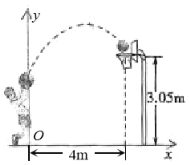
【题目】如图,一位篮球运动员在离篮圈水平距离4![]() 处跳起投篮,球运行的高度
处跳起投篮,球运行的高度![]() (
(![]() )与运行的水平距离
)与运行的水平距离![]() (
(![]() )满足解析式
)满足解析式![]() ,当球运行的水平距离为1.5
,当球运行的水平距离为1.5![]() 时,球离地面高度为3.3
时,球离地面高度为3.3![]() ,球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面距离为3.05
,球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面距离为3.05![]() .
.
(1)当球运行的水平距离为多少时,达到最大高度?最大高度为多少?
(2)若该运动员身高1.8![]() ,这次跳投时,球在他头顶上方0.25
,这次跳投时,球在他头顶上方0.25![]() 处出手,问球出手时,他跳离地面多高?
处出手,问球出手时,他跳离地面多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(Ⅰ)已知![]() ,若二次函数图象与
,若二次函数图象与![]() 轴有唯一公共点,求
轴有唯一公共点,求![]() 的值;
的值;
(Ⅱ)已知![]() .
.
(ⅰ)当![]() 时,二次函数图象与
时,二次函数图象与![]() 轴有且只有一个公共点,求
轴有且只有一个公共点,求![]() 的取值范围;
的取值范围;
(ⅱ)当![]() 时,
时,![]() 有最小值
有最小值![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 是线段
是线段![]() 的垂直平分线,交线段
的垂直平分线,交线段![]() 于点
于点![]() ,在
,在![]() 下方的直线
下方的直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,以线段
,以线段![]() 为边,在
为边,在![]() 上方作正方形
上方作正方形![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
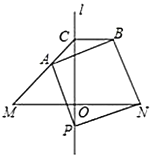
(1)设![]() ,求
,求![]() 的度数;
的度数;
(2)写出线段![]() 、
、![]() 之间的等量关系,并证明.
之间的等量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第![]() 天的成本
天的成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,并连续50天均以80元/件的价格出售,第
(天)之间的关系如图所示,并连续50天均以80元/件的价格出售,第![]() 天该产品的销售量
天该产品的销售量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]() .
.
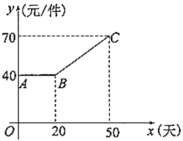
(1)第40天,该商家获得的利润是______元;
(2)设第![]() 天该商家出售该产品的利润为
天该商家出售该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在出售该产品的过程中,当天利润不低于1000元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.

已知:△ABC.
求作:BC边上的高线.
作法:如图,
①分别以A,B为圆心,大于![]() 长为半径画弧,两弧交于点D,E;
长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上( )(填推理的依据).
∵ = ,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90°( )(填推理的依据).
∴AG⊥BC
即AG就是BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com